Article contents
The Quotient Problem for Entire Functions
Published online by Cambridge University Press: 26 October 2018
Abstract
Let 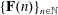 $\{\mathbf{F}(n)\}_{n\in \mathbb{N}}$ and
$\{\mathbf{F}(n)\}_{n\in \mathbb{N}}$ and 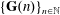 $\{\mathbf{G}(n)\}_{n\in \mathbb{N}}$ be linear recurrence sequences. It is a well-known Diophantine problem to determine the finiteness of the set
$\{\mathbf{G}(n)\}_{n\in \mathbb{N}}$ be linear recurrence sequences. It is a well-known Diophantine problem to determine the finiteness of the set 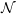 ${\mathcal{N}}$ of natural numbers such that their ratio
${\mathcal{N}}$ of natural numbers such that their ratio 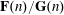 $\mathbf{F}(n)/\mathbf{G}(n)$ is an integer. In this paper we study an analogue of such a divisibility problem in the complex situation. Namely, we are concerned with the divisibility problem (in the sense of complex entire functions) for two sequences
$\mathbf{F}(n)/\mathbf{G}(n)$ is an integer. In this paper we study an analogue of such a divisibility problem in the complex situation. Namely, we are concerned with the divisibility problem (in the sense of complex entire functions) for two sequences 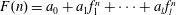 $F(n)=a_{0}+a_{1}f_{1}^{n}+\cdots +a_{l}f_{l}^{n}$ and
$F(n)=a_{0}+a_{1}f_{1}^{n}+\cdots +a_{l}f_{l}^{n}$ and 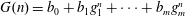 $G(n)=b_{0}+b_{1}g_{1}^{n}+\cdots +b_{m}g_{m}^{n}$, where the
$G(n)=b_{0}+b_{1}g_{1}^{n}+\cdots +b_{m}g_{m}^{n}$, where the 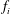 $f_{i}$ and
$f_{i}$ and 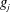 $g_{j}$ are nonconstant entire functions and the
$g_{j}$ are nonconstant entire functions and the 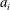 $a_{i}$ and
$a_{i}$ and 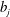 $b_{j}$ are non-zero constants except that
$b_{j}$ are non-zero constants except that 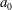 $a_{0}$ can be zero. We will show that the set
$a_{0}$ can be zero. We will show that the set 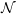 ${\mathcal{N}}$ of natural numbers such that
${\mathcal{N}}$ of natural numbers such that 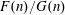 $F(n)/G(n)$ is an entire function is finite under the assumption that
$F(n)/G(n)$ is an entire function is finite under the assumption that 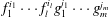 $f_{1}^{i_{1}}\cdots f_{l}^{i_{l}}g_{1}^{j_{1}}\cdots g_{m}^{j_{m}}$ is not constant for any non-trivial index set
$f_{1}^{i_{1}}\cdots f_{l}^{i_{l}}g_{1}^{j_{1}}\cdots g_{m}^{j_{m}}$ is not constant for any non-trivial index set 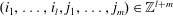 $(i_{1},\ldots ,i_{l},j_{1},\ldots ,j_{m})\in \mathbb{Z}^{l+m}$.
$(i_{1},\ldots ,i_{l},j_{1},\ldots ,j_{m})\in \mathbb{Z}^{l+m}$.
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
- 4
- Cited by

