No CrossRef data available.
Article contents
The Number of Non-cyclic Sylow Subgroups of the Multiplicative Group Modulo n
Part of:
Multiplicative number theory
Published online by Cambridge University Press: 08 June 2020
Abstract
For each positive integer n, let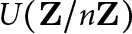 
$U(\mathbf {Z}/n\mathbf {Z})$ denote the group of units modulo n, which has order 
$\phi (n)$ (Euler’s function) and exponent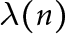 
$\lambda (n)$ (Carmichael’s function). The ratio 
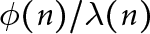$\phi (n)/\lambda (n)$ is always an integer, and a prime p divides this ratio precisely when the (unique) Sylow p-subgroup of 
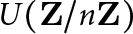$U(\mathbf {Z}/n\mathbf {Z})$ is noncyclic. Write W(n) for the number of such primes p. Banks, Luca, and Shparlinski showed that for certain constants 
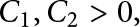$C_1, C_2>0$, for all n from a sequence of asymptotic density 1. We sharpen their result by showing that W(n) has normal order 
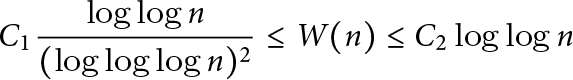$$ \begin{align*} C_1 \frac{\log\log{n}}{(\log\log\log{n})^2} \le W(n) \le C_2 \log\log{n} \end{align*} $$
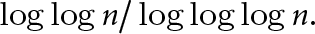$\log \log {n}/\log \log \log {n}$.
MSC classification
Secondary:
11N36: Applications of sieve methods
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
Banks, W. D., Luca, F., and Shparlinski, I. E., Arithmetic properties of 
$\phi (n)/\lambda (n)$and the structure of the multiplicative group modulo n. Comment. Math. Helv. 81(2006), 1–22. https://doi.org/10.4171/CMH/40Google Scholar
$\phi (n)/\lambda (n)$and the structure of the multiplicative group modulo n. Comment. Math. Helv. 81(2006), 1–22. https://doi.org/10.4171/CMH/40Google ScholarChang, B. and Martin, G., The smallest invariant factor of the multiplicative group. Int. J. Number Theory 16(2020), 1377–1405. https://doi.org/10.1142/S179304212500736CrossRefGoogle Scholar
Downey, J. and Martin, G., Counting multiplicative groups with prescribed subgroups. In preparation. https://arxiv.org/abs/2007.09497Google Scholar
Erdős, P., Granville, A., Pomerance, C., and Spiro, C., On the normal behavior of the iterates of some arithmetic functions. In: Analytic number theory (Allerton Park, IL, 1989), Progr. Math., 85, Birkhäuser Boston, Boston, MA, 1990, pp. 165–204. https://doi.org/10.1007/978-1-4612-3464-7_13Google Scholar
Erdős, P. and Pomerance, C., On the normal number of prime factors of $\omega (m)$. Number theory (Winnipeg, Man., 1983). Rocky Mountain J. Math. 15(1985), 343–352. https://doi.org/10.1216/RMJ-1985-15-2-343Google Scholar
$\omega (m)$. Number theory (Winnipeg, Man., 1983). Rocky Mountain J. Math. 15(1985), 343–352. https://doi.org/10.1216/RMJ-1985-15-2-343Google ScholarErdős, P., Pomerance, C., and Schmutz, E., Carmichael’s lambda function. Acta Arith. 58 (1991), 363–385. https://doi.org/10.1064/aa-58-363-385Google Scholar
Halberstam, H. and Richert, H.-E., Sieve methods. London Mathematical Society Monographs, 4, Academic Press, London-New York, 1974.Google Scholar
Martin, G. and Simpson, R. M., The universal invariant profile of the multiplicative group. In preparation.Google Scholar
Martin, G. and Troupe, L., The distribution of the number of subgroups of the multiplicative group. J. Aust. Math. Soc. 108(2020), 46–97. https://doi.org/10.1017/s1446788718000319CrossRefGoogle Scholar
Murty, M. R. and Murty, V. K., An analogue of the Erdős-Kac theorem for Fourier coefficients of modular forms. Indian J. Pure Appl. Math. 15(1984), 1090–1101.Google Scholar
Murty, M. R. and Murty, V. K., Prime divisors of Fourier coefficients of modular forms. Duke Math. J. 51(1984), 57–76. https://doi.org/10.1215/S0012-7094-84-05104-4CrossRefGoogle Scholar
Norton, K. K., On the number of restricted prime factors of an integer. I. Illinois J. Math. 20(1976), 681–705.CrossRefGoogle Scholar
Pollack, P. and Pomerance, C., Phi, Primorials, and Poisson. Illinois J. Math., to appear. https://arxiv.org/abs/2001.06727.Google Scholar
Pomerance, C., On the distribution of amicable numbers. J. Reine Angew. Math. 293(294)(1977), 217–222. https://doi.org/10.1515/crll.1977.293-294.217Google Scholar