Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-31T05:20:39.639Z Has data issue: false hasContentIssue false
  • English
  • Français

Embeddings of Müntz Spaces in 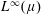$L^{\infty }(\unicode[STIX]{x1D707})$

Part of: Series expansions Special classes of linear operators Analytic spaces

Published online by Cambridge University Press:  09 January 2019

Ihab Al Alam  and
Pascal Lefèvre
Ihab Al Alam
Affiliation:
Lebanese University, Faculty of Sciences II, Department of Mathematics, Fanar-Matn 90656, Lebanon Email: ihabalam@yahoo.fr
Pascal Lefèvre
Affiliation:
Laboratoire de Mathématiques de Lens, Université Artois, 62307 Lens, France Email: pascal.lefevre@univ-artois.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we discuss the properties of the embedding operator 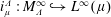$i_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6EC}}:M_{\unicode[STIX]{x1D6EC}}^{\infty }{\hookrightarrow}L^{\infty }(\unicode[STIX]{x1D707})$, where 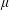$\unicode[STIX]{x1D707}$ is a positive Borel measure on 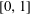$[0,1]$ and $M_{\unicode[STIX]{x1D6EC}}^{\infty }$ is a Müntz space. In particular, we compute the essential norm of this embedding. As a consequence, we recover some results of the first author. We also study the compactness (resp. weak compactness) and compute the essential norm (resp. generalized essential norm) of the embedding 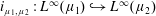$i_{\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}}:L^{\infty }(\unicode[STIX]{x1D707}_{1}){\hookrightarrow}L^{\infty }(\unicode[STIX]{x1D707}_{2})$, where 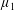$\unicode[STIX]{x1D707}_{1}$, 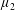$\unicode[STIX]{x1D707}_{2}$ are two positive Borel measures on [0, 1] with 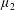$\unicode[STIX]{x1D707}_{2}$ absolutely continuous with respect to 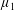$\unicode[STIX]{x1D707}_{1}$.

Keywords

Müntz spaceembeddingessential normcompact operator

MSC classification

Primary: 32C22: Embedding of analytic spaces
Secondary: 47B33: Composition operators 30B10: Power series (including lacunary series)

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 1 - 9
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work is part of the project CEDRE ESFO. The authors would like to thank the program PHC CEDRE and the Lebanese University for their support.

References

Al Alam, I., Essential norm of weighted composition operator on Müntz spaces . J. Math. Anal. Appl. 358(2009), 273–280. https://doi.org/10.1016/j.jmaa.2009.04.042.Google Scholar
Al Alam, I., Gaillard, L., Habib, G., Lefèvre, P., and Maalouf, F., Essential norms of Cesàro operators on L p and Cesàro spaces . J. Math. Anal. Appl. 467(2018), no. 2, 1038–1065. https://doi.org/10.1016/j.jmaa.2018.07.038.Google Scholar
Borwein, P. and Erdélyi, T., Polynomials and polynomial inequalities . Graduate Texts in Mathematics, 161. Springer-Verlag, New York, 1995. https://doi.org/10.1007/978-1-4612-0793-1.Google Scholar
Chalendar, I., Fricain, E., and Timotin, D., Embeddings theorems for Müntz spaces . Ann. Inst. Fourier 61(2011), 2291–2311 https://doi.org/10.5802/aif.2674.Google Scholar
Gaillard, L. and Lefèvre, P., Lacunary Müntz spaces: isomorphisms and Carleson embeddings. arxiv:1701.05807.Google Scholar
Schwartz, L., Etude des sommes d’exponentielles. Hermann, Paris, 1959.Google Scholar
Waleed Noor, S., Embeddings of Müntz spaces: Composition operators . Integral Equations Operator Theory 73(2012), 589–602. https://doi.org/10.1007/s00020-012-1965-9.Google Scholar
Waleed Noor, S. and Timotin, D., Embeddings of Müntz spaces: The Hilbertian case . Proc. Amer. Math. Soc. 141(2013), 2009–2023. https://doi.org/10.1090/S0002-9939-2012-11681-8.Google Scholar