Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-31T23:50:28.584Z Has data issue: false hasContentIssue false
  • English
  • Français

Determining sets for holomorphic functions on the symmetrized bidisk

Part of: Holomorphic convexity Linear function spaces and their duals Holomorphic functions of several complex variables Analytic spaces

Published online by Cambridge University Press:  31 January 2023

Bata Krishna Das ,
Poornendu Kumar  and
Haripada Sau
Bata Krishna Das
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India e-mail: dasb@math.iitb.ac.in bata436@gmail.com
Poornendu Kumar
Affiliation:
Department of Mathematics, Indian Institute of Science, Bengaluru 560012, India e-mail: poornendukumar@gmail.com poornenduk@iisc.ac.in
Haripada Sau*
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research, Dr. Homi Bhabha Road, Pashan, Pune, Maharashtra 411008, India
*
e-mail: haripadasau215@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A subset 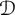${\mathcal D}$ of a domain 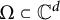$\Omega \subset {\mathbb C}^d$ is determining for an analytic function 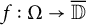$f:\Omega \to \overline {{\mathbb D}}$ if whenever an analytic function 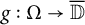$g:\Omega \rightarrow \overline {{\mathbb D}}$ coincides with f on 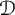${\mathcal D}$, equals to f on whole $\Omega $. This note finds several sufficient conditions for a subset of the symmetrized bidisk to be determining. For any 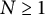$N\geq 1$, a set consisting of 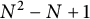$N^2-N+1$ many points is constructed which is determining for any rational inner function with a degree constraint. We also investigate when the intersection of the symmetrized bidisk intersected with some special algebraic varieties can be determining for rational inner functions.

Keywords

Rational inner functionssymmetrized bidiskdistinguished varietiesNevanlinna–Pick interpolationuniqueness varietiesdetermining setsextension problemreproducing kernel Hilbert spaces

MSC classification

Primary: 32A10: Holomorphic functions
Secondary: 32A70: Functional analysis techniques 32C25: Analytic subsets and submanifolds 32E30: Holomorphic and polynomial approximation, Runge pairs, interpolation 46E22: Hilbert spaces with reproducing kernels (=

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 3 , September 2023 , pp. 984 - 996
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

B.K.D. is supported by the Mathematical Research Impact Centric Support (MATRICS) grant, File No: MTR/2021/000560, by the Science and Engineering Research Board (SERB), Department of Science & Technology (DST), Government of India. P.K. is supported by the University Grants Commission Centre for Advanced Studies. The research works of H.S. is supported by DST-INSPIRE Faculty Fellowship DST/INSPIRE/04/2018/002458.

References

Adachi, K., Andersson, M., and Cho, H. R., $\mathrm{L}^p$  and $\mathrm{H}^p$  extensions of holomorphic functions from subvarieties of analytic polyhedra . Pacific J. Math. 189(1999), 201–210.CrossRefGoogle Scholar
Agler, J., On the representation of certain holomorphic functions define on polydisc . In: Topics in operator theory: Ernst D Hellinger memorial volume, Operator Theory: Advances and Applications, 48, Birkhauser, Basel, 1990, pp. 47–66.Google Scholar
Agler, J. and McCarthy, J. E., Nevanlinna–Pick interpolation on the bidisk . J. Reine Angew. Math. 506(1999), 191–204.CrossRefGoogle Scholar
Agler, J. and McCarthy, J. E., The three point Pick problem on the bidisk . New York J. Math. 6(2000), 227–236.Google Scholar
Agler, J. and McCarthy, J. E., Pick interpolation and Hilbert function spaces, American Mathematical Society, Providence, RI, 2002.CrossRefGoogle Scholar
Agler, J. and McCarthy, J. E., Distinguished varieties . Acta Math. 194(2005), no. 2, 133–153.CrossRefGoogle Scholar
Agler, J. and Young, N. J., A commutant lifting theorem for a domain in  ${\mathbb{C}}^2$  and spectral interpolation . J. Funct. Anal. 161(1999), no. 2, 452–477.CrossRefGoogle Scholar
Agler, J. and Young, N. J., A model theory for  $\Gamma$ -contractions . J. Operator Theory 49(2003), no. 1, 45–60.Google Scholar
Agler, J. and Young, N. J., The hyperbolic geometry of the symmetrized bidisc . J. Geom. Anal. 14(2004), 375–403.CrossRefGoogle Scholar
Agler, J. and Young, N. J., Realization of functions on the symmetrized bidisc . J. Math. Anal. Appl. 453(2017), 227–240.CrossRefGoogle Scholar
Bhattacharyya, T., Das, B. K., and Sau, H., Toeplitz operators on the symmetrized bidisc . Int. Math. Res. Not. IMRN 11(2021), 8492–8520.Google Scholar
Bhattacharyya, T., Kumar, P., and Sau, H., Distinguished varieties through the Berger–Coburn–Lebow theorem . Anal. PDE 15(2022), no. 2, 477–506.CrossRefGoogle Scholar
Bhattacharyya, T., Pal, S., and Shyam Roy, S., Dilations of $\Gamma$ -contractions by solving operator equations . Adv. Math. 230(2012), no. 2, 577–606.CrossRefGoogle Scholar
Bhattacharyya, T. and Sau, H., Holomorphic functions on the symmetrized bidisk—Realization, interpolation and extension . J. Funct. Anal. 274(2018), 504–524.CrossRefGoogle Scholar
Bhowmik, M. and Kumar, P., Bounded analytic functions on certain symmetrized domains. Preprint, 2022. arXiv:2208.07569 [math.FA]Google Scholar
Costara, C., The symmetrized bidisc and Lempert’s theorem . Bull. Lond. Math. Soc. 36(2004), 656–662.CrossRefGoogle Scholar
Dritschel, M. A., Marcantognini, S., and McCullough, S., Interpolation in semigroupoid algebras . J. Reine Angew. Math. 606(2007), 1–40.CrossRefGoogle Scholar
Dritschel, M. A. and McCullough, S., Test functions, kernels, realizations and interpolation . In: Operator theory, structured matrices, and dilations, Theta Series in Advanced Mathematics, 7, Theta, Bucharest, 2007, pp. 153–179.Google Scholar
Fischer, G., Plane algebraic curves . In: Translated from the 1994 German original by Leslie Kay. Student Mathematical Library, 15, American Mathematical Society, Providence, RI, 2001, xvi + 229 pp.Google Scholar
Jury, M., Knese, G., and McCullough, S., Nevanlinna–Pick interpolation on distinguished varieties in the bidisc . J. Funct. Anal. 262(2012), 3812–3838.CrossRefGoogle Scholar
Knese, G., Polynomials defining distinguished varieties . Trans. Amer. Math. Soc. 362(2010), 5635–5655.CrossRefGoogle Scholar
Kosiński, Ł., Three-point Nevanlinna–Pick problem in the polydisc . Proc. Lond. Math. Soc. (3) 111(2015), 887–910.CrossRefGoogle Scholar
Kosiński, Ł. and Zwonek, W., Nevanlinna–Pick problem and uniqueness of left inverses in convex domains, symmetrized bidisc and tetrablock . J. Geom. Anal. 26(2016), no. 3, 1863–1890.CrossRefGoogle Scholar
Kosiński, Ł. and Zwonek, W., Nevanlinna–Pick interpolation problem in the ball . Trans. Amer. Math. Soc. 370(2018), 3931–3947.CrossRefGoogle Scholar
Krishna Das, B., Kumar, P., and Sau, H., Distinguished varieties and the Nevanlinna–Pick interpolation problem on the symmetrized bidisk. Preprint, 2021. arXiv:2104.12392 Google Scholar
Krishna Das, B. and Sarkar, J., Andô dilations, von Neumann inequality, and distinguished varieties . J. Funct. Anal. 272(2017), no. 5, 2114–2131.Google Scholar
Maciaszek, K., Geometry of uniqueness varieties for a three-point Pick problem in $\mathrm{D}^3$ . Preprint, 2022. arXiv:2204.06612 Google Scholar
Misra, G., Shyam Roy, S., and Zhang, G., Reproducing kernel for a class of weighted Bergman spaces on the symmetrized polydisc . Proc. Amer. Math. Soc. 141(2013), no. 7, 2361–2370.CrossRefGoogle Scholar
Pal, S. and Shalit, O. M., Spectral sets and distinguished varieties in the symmetrized bidisc . J. Funct. Anal. 266(2014), 5779–5800.CrossRefGoogle Scholar
Paulsen, V. I. and Raghupathi, M., An introduction to the theory of reproducing kernel Hilbert spaces, Cambridge Studies in Advanced Mathematics, 152, Cambridge University Press, Cambridge, 2016, x+182 pp.CrossRefGoogle Scholar
Pick, G., Über die Beschränkungen analytischer Funktionen, welche durch vorgegebene Funktionswerte bewirkt werden . Math. Ann. 77(1916), 7–23.CrossRefGoogle Scholar
Rudin, W., Function theory in polydiscs, Benjamin, New York, 1969.Google Scholar
Scheinker, D., Hilbert function spaces and the Nevanlinna–Pick problem on the polydisc . J. Funct. Anal. 261(2011), 2238–2249.CrossRefGoogle Scholar
Scheinker, D., A uniqueness theorem for bounded analytic functions on the polydisc . Complex Anal. Oper. Theory 7(2013), no. 5, 1429–1436.CrossRefGoogle Scholar
Scheinker, D., Hilbert function spaces and the Nevanlinna–Pick problem on the polydisc II . J. Funct. Anal. 266(2014), 355–367.CrossRefGoogle Scholar
Stout, E. L., Bounded extensions. The case of discs in polydiscs . J. Anal. Math. 28(1975), 239–254.CrossRefGoogle Scholar