Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-31T14:39:48.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact Subsets of the Glimm Space of a C*-algebra

Published online by Cambridge University Press:  20 November 2018

Aldo J. Lazar
Aldo J. Lazar*
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv 69978, Israel e-mail: aldo@post.tau.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If $A$ is a 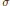$\sigma $ -unital 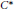${{C}^{*}}$ -algebra and $a$ is a strictly positive element of $A$ , then for every compact subset 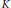$K$ of the complete regularization Glimm 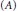$(A)$ of Prim 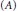$(A)$ there exists 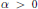$\alpha \,>\,0$ such that 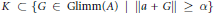$K\,\subset \,\{G\,\in \,\text{Glimm(}A\text{)}\,\text{ }\!\!|\!\!\text{ }\,\left\| a\,+\,G \right\|\,\ge \,\alpha \}$ . This extends a result of J. Dauns to all 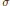$\sigma $ -unital 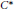${{C}^{*}}$ -algebras. However, there exist a 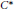${{C}^{*}}$ -algebra $A$ and a compact subset of Glimm 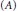$(A)$ that is not contained in any set of the form 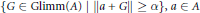$\{G\,\in \,\text{Glimm(}A\text{)}\,\text{ }\!\!|\!\!\text{ }\,\left\| a+\,G \right\|\,\ge \,\alpha \},\,a\in \,A$ and 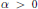$\alpha \,>\,0$ .

Keywords

46L05primitive ideal spacecomplete regularization

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 90 - 96
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Archbold, R. J., Topologies for primal ideals. J. London Math. Soc. 36 (1987), no. 3, 524–542. http://dx.doi.org/10.1112/jlms/s2-36.3.524 Google Scholar
[2] Archbold, R. J. and Somerset, D.W. B., Quasi-standard C*-algebras. Math. Proc. Cambridge Philos. Soc. 107 (1990), no. 2, 349–360. http://dx.doi.org/10.1017/S0305004100068614 Google Scholar
[3] Dauns, J., The primitive ideal space of a C*-algebra. Canad. J. Math. 26 (1974), 42–49. http://dx.doi.org/10.4153/CJM-1974-005-3 Google Scholar
[4] Dauns, J. and Hofmann, K. H., Representations of rings by sections. Memoirs of the American Mathematical Society, 83, American Mathematical Society, Providence, RI, 1968.Google Scholar
[5] Dixmier, J., C*-algebras. North-Holland Mathematical Library, 15, North-Holland, Amsterdam-New York-Oxford, 1977.Google Scholar
[6] Echterhoff, S. and Williams, D. P., Locally inner actions on C0(X)-algebras. J. Operator Theory 45 (2001), no. 1, 131–160.Google Scholar
[7] Lazar, A. J., Quotient spaces determined by algebras of continuous functions. Israel J. Math. 179 (2010), 145–155. http://dx.doi.org/10.1007/s11856-010-0075-0 Google Scholar
[8] Pedersen, G. K., C*-algebras and their automorphism groups. London Mathematical Society Monographs, 14, Academic Press, London-New York, 1979.Google Scholar