No CrossRef data available.
Article contents
A strengthening of McConnel’s theorem on permutations over finite fields
Published online by Cambridge University Press: 20 December 2024
Abstract
Let p be a prime, 
$q=p^n$, and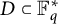 
$D \subset \mathbb {F}_q^*$. A celebrated result of McConnel states that if D is a proper subgroup of 
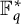$\mathbb {F}_q^*$, and 
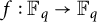$f:\mathbb {F}_q \to \mathbb {F}_q$ is a function such that 
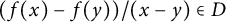$(f(x)-f(y))/(x-y) \in D$ whenever 
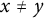$x \neq y$, then 
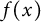$f(x)$ necessarily has the form 
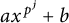$ax^{p^j}+b$. In this notes, we give a sufficient condition on D to obtain the same conclusion on f. In particular, we show that McConnel’s theorem extends if D has small doubling.
MSC classification
Primary:
11T06: Polynomials
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
References
Aguglia, A., Csajbók, B., and Weiner, Z.,
Intersecting families of graphs of functions over a finite field
. Ars Math. Contemp. 24(2024), no. 1, Article no. 4, 22 pp.Google Scholar
Asgarli, S. and Yip, C. H.,
Van Lint–MacWilliams’ conjecture and maximum cliques in Cayley graphs over finite fields
. J. Combin. Theory Ser. A 192(2022), Article no. 105667, 23 pp.CrossRefGoogle Scholar
Ball, S.,
The number of directions determined by a function over a finite field
. J. Combin. Theory Ser. A 104(2003), no. 2, 341–350.CrossRefGoogle Scholar
Blokhuis, A., Ball, S., Brouwer, A. E., Storme, L., and Szőnyi, T.,
On the number of slopes of the graph of a function defined on a finite field
. J. Combin. Theory Ser. A 86(1999), no. 1, 187–196.CrossRefGoogle Scholar
Blokhuis, A., Seress, A., and Wilbrink, H. A.,
Characterization of complete exterior sets of conics
. Combinatorica 12(1992), no. 2, 143–147.CrossRefGoogle Scholar
Bruen, A. and Levinger, B.,
A theorem on permutations of a finite field
. Canad. J. Math. 25(1973), 1060–1065.CrossRefGoogle Scholar
Carlitz, L.,
A theorem on permutations in a finite field
. Proc. Amer. Math. Soc. 11(1960), 456–459.CrossRefGoogle Scholar
Csajbók, B., Marino, G., and Polverino, O.,
A Carlitz type result for linearized polynomials
. Ars Math. Contemp. 16(2019), no. 2, 585–608.CrossRefGoogle Scholar
Göloğlu, F. and McGuire, G.,
On theorems of Carlitz and Payne on permutation polynomials over finite fields with an application to
${x}^{-1}+L(x)$
. Finite Fields Appl. 27(2014),130–142.CrossRefGoogle Scholar
${x}^{-1}+L(x)$
. Finite Fields Appl. 27(2014),130–142.CrossRefGoogle ScholarGrundhöfer, T.,
Über Abbildungen mit eingeschränktem Differenzenprodukt auf einem endlichen Körper
. Arch. Math. (Basel) 37(1981), no. 1, 59–62.CrossRefGoogle Scholar
Jones, G. A.,
Paley and the Paley graphs
. In: G. A. Jones, I. Ponomarenko, J. \v Sir\'a\v n, (eds.), Isomorphisms, symmetry and computations in algebraic graph theory, Springer Proceedings of Mathematics and Statistics, 305, Springer, Cham, 2020, pp. 155–183.CrossRefGoogle Scholar
Knarr, N. and Stroppel, M.,
Polarities and unitals in the Coulter-Matthews planes
. Des. Codes Cryptogr. 55(2010), no. 1, 9–18.CrossRefGoogle Scholar
Lenstra, H. W. Jr,
Automorphisms of finite fields
. J. Number Theory 34(1990), no. 1, 33–40.CrossRefGoogle Scholar
Lovász, L. and Schrijver, A.,
Remarks on a theorem of Rédei
. Studia Sci. Math. Hungar. 16(1983), nos. 3–4, 449–454.Google Scholar
McConnel, R.,
Pseudo-ordered polynomials over a finite field
. Acta Arith. 8(1962/63), 127–151.CrossRefGoogle Scholar
Müller, P.,
Permutation groups of prime degree, a quick proof of Burnside’s theorem
. Arch. Math. (Basel) 85(2005), no. 1, 15–17.CrossRefGoogle Scholar
Muzychuk, M. E.,
Automorphism groups of Paley graphs and cyclotomic schemes
. In: G. A. Jones, I. Ponomarenko, J. \v Sir\'a\v n, (eds.), Isomorphisms, symmetry and computations in algebraic graph theory, Springer Proceedings of Mathematics and Statistics, 305, Springer, Cham, 2020, pp. 185–194.CrossRefGoogle Scholar
Petridis, G.,
New proofs of Plünnecke-type estimates for product sets in groups
. Combinatorica 32(2012), no. 6, 721–733.CrossRefGoogle Scholar
Yip, C. H.,
Erdős–Ko–Rado theorem in Peisert-type graphs
. Canad. Math. Bull. 67(2024), no. 1, 176–187.CrossRefGoogle Scholar