Hostname: page-component-7f64f4797f-m2b9p Total loading time: 0 Render date: 2025-11-04T07:57:56.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Metric Spaces Admitting Low-distortion Embeddings into All n-dimensional Banach Spaces

Published online by Cambridge University Press:  20 November 2018

Mikhail Ostrovskii  and
Beata Randrianantoanina
Mikhail Ostrovskii
Affiliation:
Department of Mathematics and Computer Science, St. John's University, 8000 Utopia Parkway Queens, NY 11439, USA e-mail: ostrovsm@stjohns.edu
Beata Randrianantoanina
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA e-mail: randrib@miamioh.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a fixed 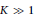$K\,\gg \,1$ and 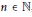$n\,\in \,\mathbb{N}$ , 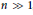$n\,\gg \,1$ we study metric spaces which admit embeddings with distortion 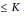$\le \,K$ into each 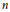$n$ -dimensional Banach space. Classical examples include spaces embeddable into log 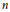$n$ -dimensional Euclidean spaces, and equilateral spaces.

We prove that good embeddability properties are preserved under the operation of metric composition of metric spaces. In particular, we prove that 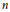$n$ -point ultrametrics can be embedded with uniformly bounded distortions into arbitrary Banach spaces of dimension 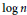$\log \,n$ .

The main result of the paper is a new example of a family of finite metric spaces which are not metric compositions of classical examples and which do embed with uniformly bounded distortion into any Banach space of dimension 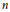$n$ . This partially answers a question of G. Schechtman.

Keywords

46B8505C1230L0546B1552A21basis constantbilipschitz embeddingdiamond graphdistortionequilateral setultrametric

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 4 , 01 August 2016 , pp. 876 - 907
Copyright
Copyright © Canadian Mathematical Society 2016

References

Refernces

[AB14] Albiac, JF. and Baudier, F., Embeddabtlity of snowfiaked metrics with applications to thenonlinear geometry of the spaces Lp and lp for 0 < p < ∞. J. Geom. Anal. 25(2015), no. 1, 1–24.http://dx.doi.org/10.1007/s12220-013-9390-0 Google Scholar
[AM83] Alon, N. and Milman, V. D., Embedding of lk∞ in finite-dimensional Banach spaces. Israel J. Math. 45(1983), no. 4, 265–280.http://dx.doi.org/10.1007/BF02804012 Google Scholar
[ABV98] Arias-de-Reyna, J., Ball, K., and Villa, R., Concentration of the distance infinite-dimensional normed spaces. Mathematika 45(1998), no. 2, 245–252.http://dx.doi.Org/10.1112/SOO255793OOO14182 Google Scholar
[Ass83] Assouad, P., Plongements lipschitziens dansRn. Bull. Soc. Math. France 111(1983), no. 4, 429–448.Google Scholar
[Bar96] Bartal, Y., Probabilistic approximation of metric spaces and its algorithmic applications. In: The 37th Annual Symposium on Foundations of Computer Science, IEEE Comput. Sci. Press, Los Alamitos, CA, 1996, pp. 184–193.Google Scholar
[Bar99] Bartal, Y., On approximating arbitrary metrices by tree metrics. STOC '98 (Dallas, TX), ACM, New York, 1999, pp. 161–168.Google Scholar
[BLMN04] Bartal, Y., Linial, N., Mendel, M., and Naor, A., Low dimensional embeddings of ultrametrics. European J. Combin. 25(2004), no. 1, 87–92.http://dx.doi.Org/10.1016/j.ejc.2OO3.O8.OO3 Google Scholar
[BLMN05] Bartal, Y., On metric Ramsey-type phenomena. Annals of Math. 162(2005), 643–709. http://dx.doi.org/10.4007/annals.2005.162.643 Google Scholar
[BM04] Bartal, Y. and Mendel, M., Dimension reduction for ultrametrics. In: Proceedings of the Fifteenth Annual ACM-SIAM Symposium on Discrete Algorithms, ACM, New York, 2004, pp. 664–665.Google Scholar
[BB91] Bastero, J. and Bernué, J., Applications of deviation inequalities on finite metric sets. Math. Nachr. 153(1991), 33–41.http://dx.doi.Org/10.1002/mana.19911530104 Google Scholar
[BBK89] Bastero, J., Bernué;s, J., and Kalton, N., Embedding ln∞-cubes in finite-dimensional 1-subsymmetric spaces. Rev. Mat. Univ. Complut. Madrid 2 (1989), suppl., 47–52.Google Scholar
[BPS95] Bastero, J., Peña, A., and Schechtman, G.,Embedding ln∞-cubes in low-dimensional Schatten classes. Geometric aspects of functional analysis (Israel, 1992-1994), 5-11, Oper. Theory Adv.Appl., 77, Birkhâuser, Basel, 1995.Google Scholar
[BFM86] Bourgain, J., Figiel, T., and Milman, V., On Hilbertian subsets of finite metric spaces. Israel J. Math. 55(1986), no. 2, 147–152.http://dx.doi.org/10.1007/BF02801990 Google Scholar
[DS13] David, G. and Snipes, M., A non-probabilistic proof ofthe Assouad embedding theorem with bounds on the dimension. Anal. Geom. Metr. Spaces 1(2013), 36–41.Google Scholar
[Dvo61] Dvoretzky, A., Some results on convex bodies and Banach spaces. In: Proc. Internat. Sympos Linear Spaces (Jerusalem, 1960), pp. 123–160, Jerusalem Academic Press, Jerusalem; Pergamon, Oxford, 1961; Announcement: A theorem on convex bodies and applications to Banach spaces, Proc. Nat. Acad. Sci. U.S.A., 45 (1959) 223-226; erratum, 1554.Google Scholar
[FL94] Füredi, Z. and Loeb, P. A., On the best constant for the Besicovitch covering theorem. Proc.Amer. Math. Soc. 121(1994), no. 4,1063–1073 http://dx.doi.org/10.1090/S0002-9939-1994-1249875-4 Google Scholar
[Glu81] Gluskin, E. D., The diameter of the Minkowski compactum is roughly equal to n. (Russian) Funktsional. Anal, i Prilozhen. 15(1981), no. 1, 72–73.http://dx.doi.Org/10.1007/BF01082381 Google Scholar
[GNRS04] Gupta, A., Newman, I., Rabinovich, Y., and Sinclair, A., Cuts, trees and l\-embeddings of graphs. Combinatorica 24(2004) 233–269.http://dx.doi.Org/10.1007/s00493-004-0015-x Google Scholar
[HeiOl] Heinonen, J. M., Lectures on Analysis on Metric Spaces, Universitext, Springer-Verlag, NewYork, 2001.Google Scholar
[HeiO3] Heinonen, J. M., Geometric embeddings of metric spaces. Report. University of Jyvâskylâ Department of Mathematics and Statistics, 90. University of Jyvâskylâ, Jyvâskylâ, 2003.http://www.math.jyu.fi/research/reports/rep90.pdf. Google Scholar
[Hugl2] Hughes, B., Trees, ultrametrics, and noncommutative geometry. Pure Appl. Math. Q. 8(2012), no. 1, 221–312. http://dx.doi.org/10.4310/PAMQ.2012.v8.n1.a11 Google Scholar
[JS09] Johnson, W. B. and Schechtman, G., Diamond graphs and super-reflexivity. J. Topol. Anal. 1(2009), no. 2, 177–189.http://dx.doi.org/10.1142/S1793525309000114 Google Scholar
[LPOl] Lang, U. and Plaut, C., Bilipschitz embeddings of metric spaces into space forms. Geom.Dedicata 87(2001), no. 1–3, 285-307.http://dx.doi.Org/10.1023/A:1012093209450 Google Scholar
[MT93] Mankiewicz, P. and Tomczak-Jaegermann, N., Embedding subspaces ofln∞ into spaces withSchauder basis. Proc. Amer. Math. Soc. 117(1993), no. 2, 459–465.Google Scholar
[MN13] Mendel, M. and Naor, A., Ultrametric subsets with large Hausdorff dimension. Invent. Math. 192(2013), no. 1, 1–54.http://dx.doi.org/10.1007/s00222-012-0402-7 Google Scholar
[Mil71] Milman, V. D., A new proof of A. Dvoretzky's theorem on cross-sections of convex bodies. (Russian) Funktsional. Anal, i Prilozhen. 5(1971), no. 4, 28–37.Google Scholar
[Mil85] Milman, V. D., Almost Euclidean quotient spaces of subspaces of a finite-dimensional normedspace. Proc. Amer. Math. Soc. 94(1985), no. 3, 445–449 http://dx.doi.org/10.1090/S0002-9939-1985-0787891-1 Google Scholar
[NN12] Naor, A. and Neiman, O., Assouad's theorem with dimension independent of the snowflaking. Rev. Mat. Iberoam. 28(2012), no. 4,1123–1142.http://dx.doi.Org/10.4171/RMI/706 Google Scholar
[Ostl4] Ostrovskii, M. I., Metric characterizations of superreflexivity in terms of word hyperbolic groups and finite graphs. Anal. Geom. Metr. Spaces 2(2014), 154–168. http://dx.doi.org/10.2478/agms-2014-0005 Google Scholar
[Rud95] Rudelson, M., Estimates of the weak distance between finite-dimensional Banach spaces. Israel J. Math. 89(1995), no. 1-3, 189–204.http://dx.doi.Org/10.1007/BF02808200 Google Scholar
[Sch84] Schikhof, W. H., Ultrametric calculus. An introduction to p-adic analysis. Cambridge Studies in Advanced Mathematics, 4. Cambridge University Press, Cambridge, 1984.Google Scholar
[Sem99] Semmes, S., Bilipschitz embeddings of metric spaces into Euclidean spaces. Publ. Mat. 43(1999), no. 2, 571–653.http://dx.doi.org/10.5565/PUBLMAT_43299_06 Google Scholar
[ShkO4] Shkarin, S. A., Isometric embedding of finite ultrametric spaces in Banach spaces. Topology Appl. 142(2004), no. 1-3, 13–17.http://dx.doi.Org/10.1016/j.topol.2003.12.002 Google Scholar
[Sza83] Szarek, S. J., The finite-dimensional basis problem with an appendix on nets of Grassmann manifolds.Acta Math. 151(1983), no. 3-4,153–179.http://dx.doi.Org/10.1007/BF02393205 Google Scholar
[ST09] Szarek, S. J. and Tomczak-Jaegermann, N., On the nontrivial projection problem. Adv. Math. 221(2009), no. 2, 331–342.http://dx.doi.Org/10.1016/j.aim.2008.12.004 Google Scholar
[Tal95] Talagrand, M., Embedding of 𝓵k ∞ and a theorem of Alon and Milman. Geometric aspects of functional analysis (Israel, 1992-1994), 289–293, Oper. Theory Adv. Appl, 77, Birkhâuser,Basel, 1995.Google Scholar