1 Introduction
Let G be a finite group and let
![]() $b_p(G)$
denote the largest degree of an irreducible Brauer character of G. Recently, Moretó (in [Reference Moretó7, Theorem 2.1]) showed that if G is solvable, then G has an abelian subgroup of index at most
$b_p(G)$
denote the largest degree of an irreducible Brauer character of G. Recently, Moretó (in [Reference Moretó7, Theorem 2.1]) showed that if G is solvable, then G has an abelian subgroup of index at most
![]() ${b_p(G)}^{43/4}$
, and there exists a characteristic abelian subgroup A of G such that
${b_p(G)}^{43/4}$
, and there exists a characteristic abelian subgroup A of G such that
![]() $|G:A|\leq {b_p(G)}^{43/2}$
. We strengthen this result by considering the irreducible monomial Brauer characters and also improve the bound substantially.
$|G:A|\leq {b_p(G)}^{43/2}$
. We strengthen this result by considering the irreducible monomial Brauer characters and also improve the bound substantially.
Moretó’s result is motivated by a result of Gluck [Reference Gluck2], who showed that in all finite groups the index of the Fitting subgroup
![]() ${\mathbf {F}}(G)$
in G is bounded by a polynomial function of
${\mathbf {F}}(G)$
in G is bounded by a polynomial function of
![]() $b(G)$
, where
$b(G)$
, where
![]() $b(G)$
is the largest degree of an irreducible character of G. For a finite solvable group G, Gluck further showed that
$b(G)$
is the largest degree of an irreducible character of G. For a finite solvable group G, Gluck further showed that
![]() $|G:{\mathbf {F}}(G)|\leq b(G)^{13/2}$
; Moretó and Wolf [Reference Moretó and Wolf9] gave the bound
$|G:{\mathbf {F}}(G)|\leq b(G)^{13/2}$
; Moretó and Wolf [Reference Moretó and Wolf9] gave the bound
![]() $|G:{\mathbf {F}}(G)|\leq b(G)^3$
. As of today, for solvable groups, the best general bound
$|G:{\mathbf {F}}(G)|\leq b(G)^3$
. As of today, for solvable groups, the best general bound
![]() $|G:{\mathbf {F}}(G)|\leq b(G)^\alpha $
was given by Yang in [Reference Yang11] with
$|G:{\mathbf {F}}(G)|\leq b(G)^\alpha $
was given by Yang in [Reference Yang11] with
![]() $\alpha ={\ln (6\cdot {(24)^{1/3}})}/{\ln 3}\approx 2.595$
.
$\alpha ={\ln (6\cdot {(24)^{1/3}})}/{\ln 3}\approx 2.595$
.
Let G be a finite solvable group,
![]() ${\operatorname {Irr}}(G)$
be the set of irreducible characters of G,
${\operatorname {Irr}}(G)$
be the set of irreducible characters of G,
![]() ${\operatorname {IBr}}(G)$
be the set of irreducible Brauer characters of G and
${\operatorname {IBr}}(G)$
be the set of irreducible Brauer characters of G and
![]() ${\operatorname {IBr}}_m(G)$
be the set of irreducible monomial Brauer characters of G. We will write
${\operatorname {IBr}}_m(G)$
be the set of irreducible monomial Brauer characters of G. We will write
![]() $b(G)$
to denote the largest degree of an ordinary irreducible character of G,
$b(G)$
to denote the largest degree of an ordinary irreducible character of G,
![]() $b_m(G)$
to denote the largest degree of an irreducible monomial character of G and
$b_m(G)$
to denote the largest degree of an irreducible monomial character of G and
![]() $b_{\textit {mp}}(G)$
to denote the largest degree of an irreducible monomial Brauer character of G. We write
$b_{\textit {mp}}(G)$
to denote the largest degree of an irreducible monomial Brauer character of G. We write
![]() ${\operatorname {acd}}(G)={\sum _{\chi \in {\operatorname {Irr}}(G)}\chi (1)}/{k(G)}$
to denote the average degree of the irreducible characters of G, where
${\operatorname {acd}}(G)={\sum _{\chi \in {\operatorname {Irr}}(G)}\chi (1)}/{k(G)}$
to denote the average degree of the irreducible characters of G, where
![]() $k(G)$
is the number of conjugacy classes of G. In the same way,
$k(G)$
is the number of conjugacy classes of G. In the same way,
![]() ${\operatorname {acd}}_p(G)$
denotes the average degree of the irreducible Brauer characters of G.
${\operatorname {acd}}_p(G)$
denotes the average degree of the irreducible Brauer characters of G.
For the average degree of the irreducible characters
![]() ${\operatorname {acd}}(G)$
, it is not true that the index of the Fitting subgroup is bounded above in terms of
${\operatorname {acd}}(G)$
, it is not true that the index of the Fitting subgroup is bounded above in terms of
![]() ${\operatorname {acd}}(G)$
. However, the index of the Fitting subgroup is bounded in terms of the average degree of the irreducible characters of G that lie over a linear character of the Fitting subgroup, and we write
${\operatorname {acd}}(G)$
. However, the index of the Fitting subgroup is bounded in terms of the average degree of the irreducible characters of G that lie over a linear character of the Fitting subgroup, and we write
![]() ${\operatorname {acd}}(G|\lambda )={\sum _{\chi \in {\operatorname {Irr}}(G|\lambda )}\chi (1)}/{k(G|\lambda )}$
. In [Reference Moretó8], Moretó proved that there exists a linear
${\operatorname {acd}}(G|\lambda )={\sum _{\chi \in {\operatorname {Irr}}(G|\lambda )}\chi (1)}/{k(G|\lambda )}$
. In [Reference Moretó8], Moretó proved that there exists a linear
![]() $\lambda \in {\operatorname {Irr}}({\mathbf {F}}(G))$
such that
$\lambda \in {\operatorname {Irr}}({\mathbf {F}}(G))$
such that
![]() $|G:{\mathbf {F}}(G)|\leq {\operatorname {acd}}(G|\lambda )^{\alpha }$
. We consider the irreducible Brauer character analogues for this case.
$|G:{\mathbf {F}}(G)|\leq {\operatorname {acd}}(G|\lambda )^{\alpha }$
. We consider the irreducible Brauer character analogues for this case.
2 Main results
Theorem 2.1. Let G be a finite solvable group. Then there exists a characteristic abelian subgroup A of G such that
![]() $|G:A|\leq {b_m(G)}^{2\alpha }\cdot b_m({\mathbf {F}}(G))^8$
.
$|G:A|\leq {b_m(G)}^{2\alpha }\cdot b_m({\mathbf {F}}(G))^8$
.
Proof. By [Reference Li, Bian and Zhang5, Theorem 4.1],
![]() $|G:{\mathbf {F}}(G)|\leq {b_m(G)}^{\alpha }$
. By [Reference Isaacs3, Theorem 12.26], there exists an abelian group
$|G:{\mathbf {F}}(G)|\leq {b_m(G)}^{\alpha }$
. By [Reference Isaacs3, Theorem 12.26], there exists an abelian group
![]() $B\le {\mathbf {F}}(G)$
such that
$B\le {\mathbf {F}}(G)$
such that
![]() $|{\mathbf {F}}(G):B|\leq {b_m({\mathbf {F}}(G))}^{4}$
(note that
$|{\mathbf {F}}(G):B|\leq {b_m({\mathbf {F}}(G))}^{4}$
(note that
![]() ${b({\mathbf {F}}(G))=b_m({\mathbf {F}}(G))}$
). Thus,
${b({\mathbf {F}}(G))=b_m({\mathbf {F}}(G))}$
). Thus,
Now, by the Chermak–Delgado theorem [Reference Isaacs4, Theorem 1.41], we conclude that G has a characteristic abelian subgroup A such that
Corollary 2.2. Suppose that all the irreducible characters of a finite solvable group G have degree at most
![]() ${b(G)}$
. Then, there exists a characteristic abelian subgroup A of G such that
${b(G)}$
. Then, there exists a characteristic abelian subgroup A of G such that
![]() $|G:A|\leq {b(G)}^{2\alpha +8}$
.
$|G:A|\leq {b(G)}^{2\alpha +8}$
.
Lemma 2.3. Let N be a normal subgroup of the finite solvable group G and suppose that there exists a Brauer character
![]() $\lambda \in {\operatorname {IBr}}(N)$
such that
$\lambda \in {\operatorname {IBr}}(N)$
such that
![]() $\lambda (1)=1$
and
$\lambda (1)=1$
and
![]() $\lambda $
is G-invariant.
$\lambda $
is G-invariant.
-
(a) Then,
 $\lambda $
is extendible to G if and only if
$\lambda $
is extendible to G if and only if
 $G'\cap N \leqslant {\operatorname {Ker}}\lambda $
.
$G'\cap N \leqslant {\operatorname {Ker}}\lambda $
. -
(b) Suppose that
 $G=NH$
and
$G=NH$
and
 $N\cap H=1$
. Then,
$N\cap H=1$
. Then,
 $\lambda $
is extendible to G.
$\lambda $
is extendible to G.
Proof. For part (a), we write
![]() $\bar {G}=G/{G'}$
. Since
$\bar {G}=G/{G'}$
. Since
![]() $N/(G'\cap N)\cong (NG')/{G'}$
and
$N/(G'\cap N)\cong (NG')/{G'}$
and
![]() $\lambda $
can be viewed as a character in
$\lambda $
can be viewed as a character in
![]() $N/(G'\cap N)$
, we have
$N/(G'\cap N)$
, we have
![]() $\bar {\lambda } \in {\operatorname {Irr}}(NG'/{G'})$
. The group
$\bar {\lambda } \in {\operatorname {Irr}}(NG'/{G'})$
. The group
![]() $\bar {G}=G/{G'}$
is abelian, so
$\bar {G}=G/{G'}$
is abelian, so
![]() $\bar {\lambda }$
is extendible to
$\bar {\lambda }$
is extendible to
![]() $\bar {G}$
and it follows that
$\bar {G}$
and it follows that
![]() $\lambda $
is extendible to G.
$\lambda $
is extendible to G.
For part (b), we write
for a module representation of
![]() $\lambda $
which affords
$\lambda $
which affords
![]() $\chi $
. For
$\chi $
. For
![]() $g\in G$
, let
$g\in G$
, let
![]() $g=ah$
, where
$g=ah$
, where
![]() $a\in N$
and
$a\in N$
and
![]() $h\in H$
. We define
$h\in H$
. We define
We can calculate directly that
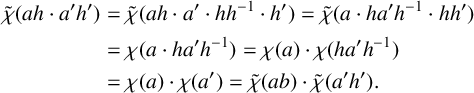 $$ \begin{align*} \tilde{\chi}(ah\cdot a'h')&=\tilde{\chi}(ah\cdot a'\cdot hh^{-1}\cdot h') =\tilde{\chi}(a\cdot ha'h^{-1}\cdot hh')\\ &=\chi(a\cdot ha'h^{-1}) =\chi(a)\cdot \chi (ha'h^{-1})\\ &=\chi(a)\cdot \chi (a') =\tilde{\chi}(ab)\cdot \tilde{\chi}(a'h'). \end{align*} $$
$$ \begin{align*} \tilde{\chi}(ah\cdot a'h')&=\tilde{\chi}(ah\cdot a'\cdot hh^{-1}\cdot h') =\tilde{\chi}(a\cdot ha'h^{-1}\cdot hh')\\ &=\chi(a\cdot ha'h^{-1}) =\chi(a)\cdot \chi (ha'h^{-1})\\ &=\chi(a)\cdot \chi (a') =\tilde{\chi}(ab)\cdot \tilde{\chi}(a'h'). \end{align*} $$
Thus,
![]() $\tilde {\chi }$
is an extension of
$\tilde {\chi }$
is an extension of
![]() $\chi $
and it follows that
$\chi $
and it follows that
![]() $\lambda $
is extendible to G.
$\lambda $
is extendible to G.
The following result strengthens [Reference Moretó7, Theorem 2.1].
Theorem 2.4. Let G be a finite solvable group and suppose that
![]() ${\mathbf {O}}_{p}(G)=1$
. Then,
${\mathbf {O}}_{p}(G)=1$
. Then,
![]() $|G:{\mathbf {F}}(G)|\leq {b_{\textit {mp}}(G)}^{\alpha }$
. Also, there exists a characteristic abelian subgroup A of G such that
$|G:{\mathbf {F}}(G)|\leq {b_{\textit {mp}}(G)}^{\alpha }$
. Also, there exists a characteristic abelian subgroup A of G such that
![]() $|G:A|\leq {b_{\textit {mp}}(G)}^{2\alpha }\cdot b_{\textit {mp}}({\mathbf {F}}(G))^8$
.
$|G:A|\leq {b_{\textit {mp}}(G)}^{2\alpha }\cdot b_{\textit {mp}}({\mathbf {F}}(G))^8$
.
Proof. Let
![]() $\bar {G} := G/{\mathbf {F}}(G)$
. Since
$\bar {G} := G/{\mathbf {F}}(G)$
. Since
![]() ${\mathbf {F}}(G/\Phi (G))= {\mathbf {F}}(G)/\Phi (G)$
, we may assume that
${\mathbf {F}}(G/\Phi (G))= {\mathbf {F}}(G)/\Phi (G)$
, we may assume that
![]() $\Phi (G)=1$
. Thus,
$\Phi (G)=1$
. Thus,
![]() ${\mathbf {F}}(G)$
is abelian. Now, G splits over the abelian normal subgroup
${\mathbf {F}}(G)$
is abelian. Now, G splits over the abelian normal subgroup
![]() ${\mathbf {F}}(G)$
. Also,
${\mathbf {F}}(G)$
. Also,
![]() ${\mathbf {F}}(G)$
is a faithful and completely reducible
${\mathbf {F}}(G)$
is a faithful and completely reducible
![]() $\bar {G}$
-module by Gaschütz’s theorem [Reference Manz and Wolf6, Theorem 1.12]. By [Reference Manz and Wolf6, Proposition 12.1],
$\bar {G}$
-module by Gaschütz’s theorem [Reference Manz and Wolf6, Theorem 1.12]. By [Reference Manz and Wolf6, Proposition 12.1],
![]() ${\operatorname {Irr}}({\mathbf {F}}(G))$
is a faithful and completely reducible
${\operatorname {Irr}}({\mathbf {F}}(G))$
is a faithful and completely reducible
![]() $\bar {G}$
-module. Since
$\bar {G}$
-module. Since
![]() ${\mathbf {O}}_{p}(G)=1$
, we have
${\mathbf {O}}_{p}(G)=1$
, we have
![]() ${\operatorname {Irr}}({\mathbf {F}}(G))={\operatorname {IBr}}({\mathbf {F}}(G))$
, and thus
${\operatorname {Irr}}({\mathbf {F}}(G))={\operatorname {IBr}}({\mathbf {F}}(G))$
, and thus
![]() ${\operatorname {IBr}}({\mathbf {F}}(G))$
is a faithful and completely reducible
${\operatorname {IBr}}({\mathbf {F}}(G))$
is a faithful and completely reducible
![]() $\bar {G}$
-module. By [Reference Yang11, Theorem 3.4], there exists
$\bar {G}$
-module. By [Reference Yang11, Theorem 3.4], there exists
![]() $\beta \in {\operatorname {IBr}}({\mathbf {F}}(G))$
such that
$\beta \in {\operatorname {IBr}}({\mathbf {F}}(G))$
such that
![]() $|\bar {G}|\le |{\bar {G}}:{\bar {I}}|^{\alpha }$
, where
$|\bar {G}|\le |{\bar {G}}:{\bar {I}}|^{\alpha }$
, where
![]() $\bar {I}=I_{\bar {G}} (\beta )=\{\bar {g}\in \bar {G} \ |\ \beta ^{\bar {g}}=\beta \}$
. Let I be the preimage of
$\bar {I}=I_{\bar {G}} (\beta )=\{\bar {g}\in \bar {G} \ |\ \beta ^{\bar {g}}=\beta \}$
. Let I be the preimage of
![]() $\bar {I}$
in G and
$\bar {I}$
in G and
![]() $I=I_G (\beta )=\{g\in G \ |\ \beta ^g=\beta \}$
. By Lemma 2.3, let
$I=I_G (\beta )=\{g\in G \ |\ \beta ^g=\beta \}$
. By Lemma 2.3, let
![]() $\widehat {\beta } \in {\operatorname {IBr}} (I|\beta )$
be an extension of
$\widehat {\beta } \in {\operatorname {IBr}} (I|\beta )$
be an extension of
![]() $\beta $
and consider
$\beta $
and consider
![]() $\chi :={\widehat {\beta }}^G\in {\operatorname {IBr}}_m(G)$
. Then,
$\chi :={\widehat {\beta }}^G\in {\operatorname {IBr}}_m(G)$
. Then,
By [Reference Isaacs3, Theorem 12.26], there exists an abelian group
![]() $B\le {\mathbf {F}}(G)$
such that
$B\le {\mathbf {F}}(G)$
such that
![]() $|{\mathbf {F}}(G):B|\leq {b({\mathbf {F}}(G))}^{4}$
. Since
$|{\mathbf {F}}(G):B|\leq {b({\mathbf {F}}(G))}^{4}$
. Since
![]() ${\mathbf {O}}_{p}(G)=1$
, we have
${\mathbf {O}}_{p}(G)=1$
, we have
![]() $b({\mathbf {F}}(G))=b_p({\mathbf {F}}(G))=b_{\textit {mp}}({\mathbf {F}}(G))$
. Thus,
$b({\mathbf {F}}(G))=b_p({\mathbf {F}}(G))=b_{\textit {mp}}({\mathbf {F}}(G))$
. Thus,
By the Chermak–Delgado theorem [Reference Isaacs4, Theorem 1.41], we conclude that G has a characteristic abelian subgroup A such that
Corollary 2.5. Suppose that all the irreducible p-Brauer characters of a finite solvable group G have degree at most
![]() ${b_{p}(G)}$
and
${b_{p}(G)}$
and
![]() ${\mathbf {O}}_{p}(G)=1$
. Then, there exists a characteristic abelian subgroup A of G such that
${\mathbf {O}}_{p}(G)=1$
. Then, there exists a characteristic abelian subgroup A of G such that
![]() $|G:A|\leq {b_{p}(G)}^{2\alpha +8}$
.
$|G:A|\leq {b_{p}(G)}^{2\alpha +8}$
.
Theorem 2.6. Let G be a finite solvable group such that
![]() ${\mathbf {O}}_{p}(G)=1$
. Then, there exists a linear
${\mathbf {O}}_{p}(G)=1$
. Then, there exists a linear
![]() $\lambda \in {\operatorname {IBr}}({\mathbf {F}}(G))$
such that
$\lambda \in {\operatorname {IBr}}({\mathbf {F}}(G))$
such that
![]() $|G:{\mathbf {F}}(G)|\leq {\operatorname {acd}}_p(G|\lambda )^{\alpha }$
.
$|G:{\mathbf {F}}(G)|\leq {\operatorname {acd}}_p(G|\lambda )^{\alpha }$
.
Proof. By Gaschütz’s theorem [Reference Manz and Wolf6, Theorem 1.12],
![]() $\bar {G}=G/{\mathbf {F}}(G)$
acts faithfully and completely reducibly on
$\bar {G}=G/{\mathbf {F}}(G)$
acts faithfully and completely reducibly on
![]() $V={\mathbf {F}}(G)/\Phi (G)$
. By [Reference Manz and Wolf6, Proposition 12.1],
$V={\mathbf {F}}(G)/\Phi (G)$
. By [Reference Manz and Wolf6, Proposition 12.1],
![]() ${\operatorname {Irr}}(V)$
is a faithful and completely reducible
${\operatorname {Irr}}(V)$
is a faithful and completely reducible
![]() $\bar {G}$
-module. Since
$\bar {G}$
-module. Since
![]() ${\mathbf {O}}_{p}(G)=1$
, we have
${\mathbf {O}}_{p}(G)=1$
, we have
![]() $p\nmid |{\mathbf {F}}(G)|$
and
$p\nmid |{\mathbf {F}}(G)|$
and
![]() ${\operatorname {Irr}}(V)={\operatorname {IBr}}(V)$
. Applying [Reference Yang11, Theorem 3.4] to this action, we deduce that there exists
${\operatorname {Irr}}(V)={\operatorname {IBr}}(V)$
. Applying [Reference Yang11, Theorem 3.4] to this action, we deduce that there exists
![]() ${\lambda \in {\operatorname {IBr}}(V)}$
such that
${\lambda \in {\operatorname {IBr}}(V)}$
such that
By Clifford’s correspondence [Reference Navarro10, Theorem 8.9], all the characters in
![]() ${\operatorname {IBr}}(G|\lambda )$
are induced from irreducible Brauer characters of
${\operatorname {IBr}}(G|\lambda )$
are induced from irreducible Brauer characters of
![]() $I_G(\lambda )$
. In particular, if
$I_G(\lambda )$
. In particular, if
![]() $\chi \in {\operatorname {IBr}}(G|\lambda )$
, then
$\chi \in {\operatorname {IBr}}(G|\lambda )$
, then
It follows that
As usual, if G is a group, then
![]() ${\mathbf {O}}_{p'}(G)$
is the largest normal
${\mathbf {O}}_{p'}(G)$
is the largest normal
![]() $p'$
-subgroup of G. We define
$p'$
-subgroup of G. We define
![]() ${\mathbf {O}}_{p' p}(G)$
to be the subgroup of G such that
${\mathbf {O}}_{p' p}(G)$
to be the subgroup of G such that
![]() ${\mathbf {O}}_{p' p}(G)/{\mathbf {O}}_{p'}(G)={\mathbf {O}}_{p}(G/{\mathbf {O}}_{p'}(G))$
. If
${\mathbf {O}}_{p' p}(G)/{\mathbf {O}}_{p'}(G)={\mathbf {O}}_{p}(G/{\mathbf {O}}_{p'}(G))$
. If
![]() $N\unlhd G$
and
$N\unlhd G$
and
![]() $\lambda \in {\operatorname {Irr}}(N)$
, we write
$\lambda \in {\operatorname {Irr}}(N)$
, we write
![]() $C_G(\lambda )$
to be the inertia subgroup in G of
$C_G(\lambda )$
to be the inertia subgroup in G of
![]() $\lambda $
. We write
$\lambda $
. We write
![]() ${\operatorname {Irr}}_{mp'}(G)$
to be the set of all the irreducible monomial
${\operatorname {Irr}}_{mp'}(G)$
to be the set of all the irreducible monomial
![]() $p'$
-degree characters of G and
$p'$
-degree characters of G and
![]() $b_{mp'}(G)$
to be the largest degree of the irreducible characters in
$b_{mp'}(G)$
to be the largest degree of the irreducible characters in
![]() ${\operatorname {Irr}}_{mp'}(G)$
.
${\operatorname {Irr}}_{mp'}(G)$
.
Lemma 2.7 [Reference Moretó7, Lemma 3.1].
Let
![]() $G=NH$
, where
$G=NH$
, where
![]() $N\unlhd G$
and
$N\unlhd G$
and
![]() $N\cap H=1$
. If
$N\cap H=1$
. If
![]() $\lambda \in {\operatorname {Irr}}(N)$
is linear and G-invariant, then
$\lambda \in {\operatorname {Irr}}(N)$
is linear and G-invariant, then
![]() $\lambda $
is extendible to G.
$\lambda $
is extendible to G.
Lemma 2.8. Let
![]() $G=HV$
, where
$G=HV$
, where
![]() $V\unlhd G$
is an elementary abelian p-group,
$V\unlhd G$
is an elementary abelian p-group,
![]() $H\cap V=1$
, and H acts faithfully and completely reducibly on V. Then,
$H\cap V=1$
, and H acts faithfully and completely reducibly on V. Then,
![]() $|{\mathbf {F}}(H)|\leq b_{mp'}(G)^2$
.
$|{\mathbf {F}}(H)|\leq b_{mp'}(G)^2$
.
Proof. Let P be a Sylow p-subgroup of H and let
![]() $F={\mathbf {F}}(H)$
. Set
$F={\mathbf {F}}(H)$
. Set
![]() $K=PF$
. We note that K acts faithfully on V, so
$K=PF$
. We note that K acts faithfully on V, so
![]() ${\mathbf {F}}(KV)=V$
. This implies that K acts faithfully and completely reducibly on
${\mathbf {F}}(KV)=V$
. This implies that K acts faithfully and completely reducibly on
![]() ${\operatorname {Irr}}(V)$
. By [Reference Dolfi and Navarro1, Theorem 1.1], there exists a P-invariant
${\operatorname {Irr}}(V)$
. By [Reference Dolfi and Navarro1, Theorem 1.1], there exists a P-invariant
![]() $\lambda \in {\operatorname {Irr}}(V)$
such that
$\lambda \in {\operatorname {Irr}}(V)$
such that
![]() $|F:C_F(\lambda )|\geq \sqrt {|F|}$
. Clifford’s correspondence implies that if
$|F:C_F(\lambda )|\geq \sqrt {|F|}$
. Clifford’s correspondence implies that if
![]() $\widehat {\lambda }\in {\operatorname {Irr}}(G|\lambda )$
, then
$\widehat {\lambda }\in {\operatorname {Irr}}(G|\lambda )$
, then
![]() ${\widehat {\lambda }(1)\geq \sqrt {|F|}}$
.
${\widehat {\lambda }(1)\geq \sqrt {|F|}}$
.
By Lemma 2.7,
![]() $\lambda $
can be extended to
$\lambda $
can be extended to
![]() $C_G(\lambda )$
. Since
$C_G(\lambda )$
. Since
![]() $P\leq C_G(\lambda )$
, by using Clifford’s correspondence again, all the characters in
$P\leq C_G(\lambda )$
, by using Clifford’s correspondence again, all the characters in
![]() ${\operatorname {Irr}}(G|\lambda )$
are induced from irreducible characters of
${\operatorname {Irr}}(G|\lambda )$
are induced from irreducible characters of
![]() $C_G(\lambda )$
. We deduce that there exists a
$C_G(\lambda )$
. We deduce that there exists a
![]() $p'$
-degree character
$p'$
-degree character
![]() $\widehat {\lambda }\in {\operatorname {Irr}}(G|\lambda )$
. Then, we have a
$\widehat {\lambda }\in {\operatorname {Irr}}(G|\lambda )$
. Then, we have a
![]() $p'$
-degree character
$p'$
-degree character
![]() $\chi :=\widehat {\lambda }^{G}\in {\operatorname {Irr}}_m(G)$
and
$\chi :=\widehat {\lambda }^{G}\in {\operatorname {Irr}}_m(G)$
and
![]() $\chi (1)\geq \sqrt {|F|}$
. Hence,
$\chi (1)\geq \sqrt {|F|}$
. Hence,
Thus, we deduce that
![]() $|{\mathbf {F}}(H)|\leq b_{mp'}(G)^2$
.
$|{\mathbf {F}}(H)|\leq b_{mp'}(G)^2$
.
Theorem 2.9. Let G be a solvable group. Then,
![]() $|G:{\mathbf {O}}_{p',p}(G)|\leq b_{mp'}(G)^{13/2}$
.
$|G:{\mathbf {O}}_{p',p}(G)|\leq b_{mp'}(G)^{13/2}$
.
Proof. Without loss of generality, we may assume that
![]() ${\mathbf {O}}_{p'}(G)=1$
. We write
${\mathbf {O}}_{p'}(G)=1$
. We write
![]() ${V={\mathbf {O}}_{p}(G)}$
and note that V is the Fitting subgroup G. By Gaschütz’s theorem, we may assume that
${V={\mathbf {O}}_{p}(G)}$
and note that V is the Fitting subgroup G. By Gaschütz’s theorem, we may assume that
![]() $\Phi (G)=1$
, so that V is elementary abelian. We write
$\Phi (G)=1$
, so that V is elementary abelian. We write
![]() $G=HV$
with
$G=HV$
with
![]() ${H\cap V=1}$
and note that H acts faithfully and completely reducibly on V. Let
${H\cap V=1}$
and note that H acts faithfully and completely reducibly on V. Let
![]() $F={\mathbf {F}}(H)$
. Then,
$F={\mathbf {F}}(H)$
. Then,
![]() $|{\mathbf {F}}(H)|\leq b_{mp'}(G)^2$
by Lemma 2.8.
$|{\mathbf {F}}(H)|\leq b_{mp'}(G)^2$
by Lemma 2.8.
From [Reference Manz and Wolf6, Theorem 3.5],
![]() $|H:F|\leq |F|^{9/4}$
, and thus
$|H:F|\leq |F|^{9/4}$
, and thus


