1. Introduction
All groups considered in this paper are finite unless otherwise stated. To study the structure of a group, one can look at the invariants of some graphs whose vertices are the elements of the group and whose edges reveal some properties of the group itself. More precisely, if G is a group and
![]() ${\mathcal {B}}$
is a class of groups, the
${\mathcal {B}}$
is a class of groups, the
![]() ${\mathcal {B}}$
-graph associated with G, denoted by
${\mathcal {B}}$
-graph associated with G, denoted by
![]() $\Gamma _{{\mathcal {B}}}(G)$
, is a simple and undirected graph whose vertices are the elements of G, and there is an edge between two elements x and y of G if the subgroup generated by x and y is a
$\Gamma _{{\mathcal {B}}}(G)$
, is a simple and undirected graph whose vertices are the elements of G, and there is an edge between two elements x and y of G if the subgroup generated by x and y is a
![]() ${\mathcal {B}}$
-group.
${\mathcal {B}}$
-group.
Several features of a finite group can be detected by analysing the invariants of its
![]() ${\mathcal {B}}$
-graph. We refer to [Reference Cameron5] for a survey on this topic and to [Reference Grazian, Lucchini and Monetta10, Reference Grazian and Monetta11] for related work. Recent papers deal with the investigation of the (closed) neighbourhood
${\mathcal {B}}$
-graph. We refer to [Reference Cameron5] for a survey on this topic and to [Reference Grazian, Lucchini and Monetta10, Reference Grazian and Monetta11] for related work. Recent papers deal with the investigation of the (closed) neighbourhood
![]() ${\mathcal {I}}_{\mathcal {B}}(x)$
of a vertex x in
${\mathcal {I}}_{\mathcal {B}}(x)$
of a vertex x in
![]() $\Gamma _{{\mathcal {B}}}(G)$
, that is, the set of all y in G such that x and y generate a
$\Gamma _{{\mathcal {B}}}(G)$
, that is, the set of all y in G such that x and y generate a
![]() ${\mathcal {B}}$
-group. When
${\mathcal {B}}$
-group. When
![]() ${\mathcal {B}}$
is the class of abelian groups, then
${\mathcal {B}}$
is the class of abelian groups, then
![]() ${\mathcal {I}}_{\mathcal {B}}(x)$
coincides with the centraliser of x in G, thus
${\mathcal {I}}_{\mathcal {B}}(x)$
coincides with the centraliser of x in G, thus
![]() ${\mathcal {I}}_{\mathcal {B}}(x)$
is a subgroup. However, in general this is not the case when
${\mathcal {I}}_{\mathcal {B}}(x)$
is a subgroup. However, in general this is not the case when
![]() ${\mathcal {B}}$
is distinct from the class of abelian groups. Nevertheless, even though
${\mathcal {B}}$
is distinct from the class of abelian groups. Nevertheless, even though
![]() ${\mathcal {I}}_{\mathcal {B}}(x)$
is not a subgroup of G in general, it can happen that the characteristics of a single neighbourhood in a
${\mathcal {I}}_{\mathcal {B}}(x)$
is not a subgroup of G in general, it can happen that the characteristics of a single neighbourhood in a
![]() ${\mathcal {B}}$
-graph could affect the structure of the whole group G. For instance, when
${\mathcal {B}}$
-graph could affect the structure of the whole group G. For instance, when
![]() ${\mathcal {B}}$
coincides with the class
${\mathcal {B}}$
coincides with the class
![]() $\mathcal S$
of soluble groups, it has been shown that the combinatorial properties, as well as arithmetic ones, of
$\mathcal S$
of soluble groups, it has been shown that the combinatorial properties, as well as arithmetic ones, of
![]() ${\mathcal {I}}_{\mathcal {B}}(x)$
may force the whole group to be abelian or nilpotent (see [Reference Akbari, Delizia and Monetta2, Reference Akbari, Lewis, Mirzajani and Moghaddamfar3] for more details).
${\mathcal {I}}_{\mathcal {B}}(x)$
may force the whole group to be abelian or nilpotent (see [Reference Akbari, Delizia and Monetta2, Reference Akbari, Lewis, Mirzajani and Moghaddamfar3] for more details).
Here we start by considering the class
![]() ${\mathcal {C}}$
of all cyclic groups. Cameron in [Reference Cameron5] calls the graph
${\mathcal {C}}$
of all cyclic groups. Cameron in [Reference Cameron5] calls the graph
![]() $\Gamma _{{\mathcal {C}}} (G)$
the enhanced power graph. The term enhanced power graph appears to have originated in [Reference Aalipour, Akbari, Cameron, Nikandish and Shaveisi1]. However, this graph was first studied in [Reference Imperatore, Bianchi, Longobardi, Maj and Scoppola12] under the name cyclic graph. Further investigations under this name occurred in [Reference Imperatore and Lewis13]. Recently, this graph has been investigated in [Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell6–Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell8] and there are still several open questions, as described in [Reference Ma, Kelarev, Lin and Wang15].
$\Gamma _{{\mathcal {C}}} (G)$
the enhanced power graph. The term enhanced power graph appears to have originated in [Reference Aalipour, Akbari, Cameron, Nikandish and Shaveisi1]. However, this graph was first studied in [Reference Imperatore, Bianchi, Longobardi, Maj and Scoppola12] under the name cyclic graph. Further investigations under this name occurred in [Reference Imperatore and Lewis13]. Recently, this graph has been investigated in [Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell6–Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell8] and there are still several open questions, as described in [Reference Ma, Kelarev, Lin and Wang15].
Our interest in
![]() $\Gamma _{{\mathcal {C}}} (G)$
chiefly concerns the cardinality of
$\Gamma _{{\mathcal {C}}} (G)$
chiefly concerns the cardinality of
![]() ${\mathcal {I}}_{\mathcal {C}} (x)$
, discussing the possible values that can occur for
${\mathcal {I}}_{\mathcal {C}} (x)$
, discussing the possible values that can occur for
![]() $|{\mathcal {I}}_{\mathcal {C}} (x)|$
when x belongs to a p-group G. Denote by
$|{\mathcal {I}}_{\mathcal {C}} (x)|$
when x belongs to a p-group G. Denote by
![]() $n_G$
the maximum of the sizes of all
$n_G$
the maximum of the sizes of all
![]() ${\mathcal {I}}_{\mathcal {C}}(x)$
for
${\mathcal {I}}_{\mathcal {C}}(x)$
for
![]() $x \in G \setminus \{1\}$
. Then clearly
$x \in G \setminus \{1\}$
. Then clearly
where
![]() $\exp (G)$
denotes the exponent of the group G. Whenever G has a nontrivial universal vertex, that is, a nontrivial element adjacent to any element of G,
$\exp (G)$
denotes the exponent of the group G. Whenever G has a nontrivial universal vertex, that is, a nontrivial element adjacent to any element of G,
![]() $n_G=|G|$
. These groups have been characterised in the soluble case in [Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell8]. Our first goal is to characterise p-groups G with
$n_G=|G|$
. These groups have been characterised in the soluble case in [Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell8]. Our first goal is to characterise p-groups G with
![]() $n_G = \exp (G)$
. Indeed we prove the following result.
$n_G = \exp (G)$
. Indeed we prove the following result.
Theorem 1.1. Let G be a finite p-group. Then
![]() $n_G=\exp (G)$
if and only if G is cyclic, or
$n_G=\exp (G)$
if and only if G is cyclic, or
![]() $\exp (G)=p$
, or G is a dihedral
$\exp (G)=p$
, or G is a dihedral
![]() $2$
-group.
$2$
-group.
It is worth mentioning that a problem connected to closed neighbourhoods has been addressed in [Reference Kumar, Parveen and Singh14]. Going further, one may ask what is the second value that can occur for
![]() $n_G$
, and the answer is given by the following proposition.
$n_G$
, and the answer is given by the following proposition.
Proposition 1.2. Let G be a p-group and assume
![]() $n_G> \exp (G)$
. Then we have
$n_G> \exp (G)$
. Then we have
![]() ${n_G \geq p^{\alpha + 1} - p^{\alpha } + p^{\alpha -1}}$
.
${n_G \geq p^{\alpha + 1} - p^{\alpha } + p^{\alpha -1}}$
.
We point out that the bound in Theorem 1.2 is sharp in some sense. Indeed, for
![]() $G=C_{p^2} \times C_p$
we have
$G=C_{p^2} \times C_p$
we have
![]() $n_G = p^{3} - p^{2} + p$
, where
$n_G = p^{3} - p^{2} + p$
, where
![]() $C_k$
denotes the cyclic group of order k.
$C_k$
denotes the cyclic group of order k.
2. The cyclic graph
In this section we will deal with the enhanced power graph of a group, or what we like to call the cyclic graph of a group. Recall that the cyclic graph of a group G, denoted by
![]() $\Delta (G)$
, is the graph whose vertex set is
$\Delta (G)$
, is the graph whose vertex set is
![]() $G \setminus \{1\}$
, and two distinct elements
$G \setminus \{1\}$
, and two distinct elements
![]() $x,y$
of G are adjacent if and only if
$x,y$
of G are adjacent if and only if
![]() $\langle x, y\rangle $
is cyclic. When x and y are adjacent we will write
$\langle x, y\rangle $
is cyclic. When x and y are adjacent we will write
![]() $x \sim y$
. We denote by
$x \sim y$
. We denote by
![]() $n_G$
the maximum of the sizes of all
$n_G$
the maximum of the sizes of all
![]() ${\mathcal {I}}_{\mathcal {C}} (x)$
for
${\mathcal {I}}_{\mathcal {C}} (x)$
for
![]() $x \in G \setminus \{1\}$
. We begin with the following useful lemma.
$x \in G \setminus \{1\}$
. We begin with the following useful lemma.
Lemma 2.1. Let p be a prime and let G be a p-group. Then there exists an element
![]() $z \in G$
of order p such that
$z \in G$
of order p such that
![]() $|{\mathcal {I}}_{\mathcal {C}} (z)| = n_G$
.
$|{\mathcal {I}}_{\mathcal {C}} (z)| = n_G$
.
Proof. Observe that there exists an element
![]() $x \in G$
such that
$x \in G$
such that
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (x)| = n_G$
. If
$|{\mathcal {I}}_{{\mathcal {C}}} (x)| = n_G$
. If
![]() $o (x) = p$
, then we are done. Therefore, we assume that
$o (x) = p$
, then we are done. Therefore, we assume that
![]() $o (x) = p^k$
, where k is an integer so that
$o (x) = p^k$
, where k is an integer so that
![]() $k \geq 2$
. Take
$k \geq 2$
. Take
![]() $z = x^{p^{k-1}}$
, and observe that x and z belong to the same connected component
$z = x^{p^{k-1}}$
, and observe that x and z belong to the same connected component
![]() $\Upsilon $
in
$\Upsilon $
in
![]() $\Delta (G)$
, and that z is the only element of order p in
$\Delta (G)$
, and that z is the only element of order p in
![]() $\Upsilon $
. By [Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell6, Lemma 2.2],
$\Upsilon $
. By [Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell6, Lemma 2.2],
![]() $z \sim y$
for any element
$z \sim y$
for any element
![]() $y \in \Upsilon $
, and so
$y \in \Upsilon $
, and so
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (z)| \geq |{\mathcal {I}}_{{\mathcal {C}}} (x)|=n_G$
, which implies
$|{\mathcal {I}}_{{\mathcal {C}}} (z)| \geq |{\mathcal {I}}_{{\mathcal {C}}} (x)|=n_G$
, which implies
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (z)| = n_G$
.
$|{\mathcal {I}}_{{\mathcal {C}}} (z)| = n_G$
.
By Lemma 2.1 and [Reference Costanzo, Lewis, Schmidt, Tsegaye and Udell6, Lemma 2.2], one can easily see that
![]() $n_G = |\Upsilon | - 1$
, where
$n_G = |\Upsilon | - 1$
, where
![]() $\Upsilon $
is a connected component of
$\Upsilon $
is a connected component of
![]() $\Delta (G)$
containing a vertex of degree
$\Delta (G)$
containing a vertex of degree
![]() $n_G$
.
$n_G$
.
2.1. Abelian p-groups
In this subsection, we focus on Abelian p-groups. In the next lemma, we compute
![]() $n_G$
when G is a nontrivial cyclic group.
$n_G$
when G is a nontrivial cyclic group.
Lemma 2.2. If G is a nontrivial cyclic group, then
![]() $n_G=|G|$
.
$n_G=|G|$
.
Proof. Let
![]() $x \in G$
such that
$x \in G$
such that
![]() $G= \langle x \rangle $
. Since
$G= \langle x \rangle $
. Since
![]() $o(x)=|G|$
and
$o(x)=|G|$
and
![]() $G \setminus \langle x \rangle = \emptyset $
, we conclude that
$G \setminus \langle x \rangle = \emptyset $
, we conclude that
![]() $n_G=|G|$
.
$n_G=|G|$
.
We next compute
![]() $n_G$
when G is a p-group having exponent p.
$n_G$
when G is a p-group having exponent p.
Lemma 2.3. Let p be a prime and let G be a p-group of exponent p. Then
![]() $n_G = p$
.
$n_G = p$
.
Proof. If G is a cyclic group of order p, then the result follows from Lemma 2.2. Assume that G is not cyclic, and consider an element
![]() $x \in G$
such that
$x \in G$
such that
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (x)| = n_G$
. As
$|{\mathcal {I}}_{{\mathcal {C}}} (x)| = n_G$
. As
![]() $o(x) = p$
, we have
$o(x) = p$
, we have
![]() $n_G \geq p$
.
$n_G \geq p$
.
Now observe that if
![]() $y \in G \setminus \langle x \rangle $
, then
$y \in G \setminus \langle x \rangle $
, then
![]() $ \langle x, y \rangle $
is not cyclic. Indeed, arguing by contradiction, let
$ \langle x, y \rangle $
is not cyclic. Indeed, arguing by contradiction, let
![]() $z \in G$
be such that
$z \in G$
be such that
![]() $\langle x, y \rangle = \langle z \rangle $
. Since G has exponent p, there exist
$\langle x, y \rangle = \langle z \rangle $
. Since G has exponent p, there exist
![]() $i , j \in \{1, \ldots , p-1\}$
such that
$i , j \in \{1, \ldots , p-1\}$
such that
![]() $x = z^i$
and
$x = z^i$
and
![]() $y = z^j$
. Therefore, from
$y = z^j$
. Therefore, from
![]() $(i,p) = 1$
it follows that
$(i,p) = 1$
it follows that
![]() $\langle x \rangle = \langle z^i \rangle = \langle z \rangle $
and
$\langle x \rangle = \langle z^i \rangle = \langle z \rangle $
and
![]() $y \in \langle x \rangle $
, a contradiction. Hence, we conclude that
$y \in \langle x \rangle $
, a contradiction. Hence, we conclude that
![]() $n_G = p$
.
$n_G = p$
.
We now show that if G is a noncyclic abelian group whose exponent is larger than p, then
![]() $n_G$
is larger than the exponent of G.
$n_G$
is larger than the exponent of G.
Lemma 2.4. Let p be a prime and let G be a noncyclic abelian p-group of exponent
![]() $exp(G) = p^{\alpha }$
, where
$exp(G) = p^{\alpha }$
, where
![]() $\alpha \geq 2$
. Then
$\alpha \geq 2$
. Then
![]() $n_G \geq p^{\alpha + 1} - p^{\alpha } + p^{\alpha -1}$
. As a consequence,
$n_G \geq p^{\alpha + 1} - p^{\alpha } + p^{\alpha -1}$
. As a consequence,
![]() ${n_G> \exp (G)}$
.
${n_G> \exp (G)}$
.
Proof. As G is abelian, we may assume
where
![]() $r\geq 2$
,
$r\geq 2$
,
![]() $1 \leq \alpha _1 \leq \cdots \leq \alpha _r=\alpha $
and
$1 \leq \alpha _1 \leq \cdots \leq \alpha _r=\alpha $
and
![]() $C_{p^{\alpha _i}}=\langle x_i\rangle $
is a cyclic group of order
$C_{p^{\alpha _i}}=\langle x_i\rangle $
is a cyclic group of order
![]() $p^{\alpha _i}$
.
$p^{\alpha _i}$
.
If
![]() $\alpha _{r-1}=1$
, then the vertex
$\alpha _{r-1}=1$
, then the vertex
![]() $x_r^{p^{\alpha -1}}$
is adjacent to
$x_r^{p^{\alpha -1}}$
is adjacent to
![]() $p^{\alpha }-2$
nontrivial elements of
$p^{\alpha }-2$
nontrivial elements of
![]() $\langle x_r \rangle $
and to any element of the form
$\langle x_r \rangle $
and to any element of the form
![]() $x_{r-1}^i x_r^k$
, where
$x_{r-1}^i x_r^k$
, where
![]() $i=1, \ldots , p-1$
and k is a positive integer less than
$i=1, \ldots , p-1$
and k is a positive integer less than
![]() $p^{\alpha }$
and coprime with p. Hence, there are precisely
$p^{\alpha }$
and coprime with p. Hence, there are precisely
![]() $p^{\alpha } - p^{\alpha - 1}$
choices for k, which implies
$p^{\alpha } - p^{\alpha - 1}$
choices for k, which implies
If
![]() $\alpha _{r-1}>1$
, then one can consider the subgroup
$\alpha _{r-1}>1$
, then one can consider the subgroup
![]() $\langle x_r^{p^{\alpha _{r-1} - 1}}, x_r \rangle $
, arguing as in the previous case.
$\langle x_r^{p^{\alpha _{r-1} - 1}}, x_r \rangle $
, arguing as in the previous case.
We now collect these lemmas in a proposition where we note that, for an abelian p-group G,
![]() $n_G$
equals the exponent of G if and only if G is cyclic or elementary abelian.
$n_G$
equals the exponent of G if and only if G is cyclic or elementary abelian.
Proposition 2.5. Let p be a prime and let G be an abelian p-group. Then
![]() ${n_G=\exp (G)}$
if and only if G is either cyclic or elementary abelian.
${n_G=\exp (G)}$
if and only if G is either cyclic or elementary abelian.
2.2. Nonabelian p-groups
We now shift our focus to nonabelian p-groups. When p is a prime, we take
![]() $\alpha $
to be an integer greater than
$\alpha $
to be an integer greater than
![]() $1$
when p is odd and an integer greater than
$1$
when p is odd and an integer greater than
![]() $2$
when
$2$
when
![]() $p = 2$
. We denote by
$p = 2$
. We denote by
![]() $M_{p^{\alpha +1}}$
the group
$M_{p^{\alpha +1}}$
the group
Going further, we respectively denote by
![]() $D_{2^{\alpha +1}}$
,
$D_{2^{\alpha +1}}$
,
![]() $S_{p^{\alpha +1}}$
and
$S_{p^{\alpha +1}}$
and
![]() $Q_{2^{\alpha +1}}$
the dihedral, semidihedral and generalised quaternion groups given by the following presentations:
$Q_{2^{\alpha +1}}$
the dihedral, semidihedral and generalised quaternion groups given by the following presentations:
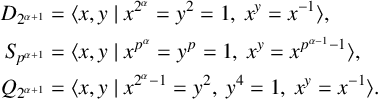 $$ \begin{align*} D_{2^{\alpha +1}}& = \langle x,y \mid x^{2^{\alpha}}=y^2=1, \ x^y=x^{-1} \rangle, \\ S_{p^{\alpha +1}} &= \langle x,y \mid x^{p^{\alpha}}=y^p=1, \ x^y=x^{p^{\alpha-1}-1} \rangle, \\ Q_{2^{\alpha +1}} &= \langle x,y \mid x^{2^{\alpha}-1}=y^2, \ y^4=1,\ x^y=x^{-1} \rangle. \end{align*} $$
$$ \begin{align*} D_{2^{\alpha +1}}& = \langle x,y \mid x^{2^{\alpha}}=y^2=1, \ x^y=x^{-1} \rangle, \\ S_{p^{\alpha +1}} &= \langle x,y \mid x^{p^{\alpha}}=y^p=1, \ x^y=x^{p^{\alpha-1}-1} \rangle, \\ Q_{2^{\alpha +1}} &= \langle x,y \mid x^{2^{\alpha}-1}=y^2, \ y^4=1,\ x^y=x^{-1} \rangle. \end{align*} $$
The characterisation of nonabelian p-groups with a cyclic maximal subgroup is well known (see [Reference Gorenstein9]).
Theorem 2.6. Let p be a prime and let G be a nonabelian p-group of order
![]() $p^{\alpha +1}$
with a cyclic subgroup of order
$p^{\alpha +1}$
with a cyclic subgroup of order
![]() $p^{\alpha }$
.
$p^{\alpha }$
.
-
(i) If p is odd then G is isomorphic to
 $M_{p^{\alpha + 1}}$
.
$M_{p^{\alpha + 1}}$
. -
(ii) If
 $p=2$
and
$p=2$
and
 $\alpha =2$
, then G is isomorphic to either
$\alpha =2$
, then G is isomorphic to either
 $D_{8}$
or
$D_{8}$
or
 $Q_{8}$
.
$Q_{8}$
. -
(iii) If
 $p=2$
and
$p=2$
and
 $\alpha>3$
, then G is isomorphic to either
$\alpha>3$
, then G is isomorphic to either
 $M_{2^{\alpha + 1}}$
,
$M_{2^{\alpha + 1}}$
,
 $D_{2^{\alpha + 1}}$
,
$D_{2^{\alpha + 1}}$
,
 $Q_{2^{\alpha + 1}}$
or
$Q_{2^{\alpha + 1}}$
or
 $S_{2^{\alpha + 1}}$
.
$S_{2^{\alpha + 1}}$
.
We compute
![]() $n_G$
for nonabelian p-groups with a maximal cyclic subgroup of index p.
$n_G$
for nonabelian p-groups with a maximal cyclic subgroup of index p.
Proposition 2.7. Let p be a prime and let G be a p-group of order
![]() $p^{\alpha +1}$
. Assume that G has a maximal cyclic subgroup of order
$p^{\alpha +1}$
. Assume that G has a maximal cyclic subgroup of order
![]() $p^{\alpha }$
. Then
$p^{\alpha }$
. Then
![]() $n_G = \exp (G)$
if and only if either G is cyclic, or
$n_G = \exp (G)$
if and only if either G is cyclic, or
![]() $\exp (G) = p$
, or
$\exp (G) = p$
, or
![]() $G \simeq D_{2^{\alpha +1}}$
.
$G \simeq D_{2^{\alpha +1}}$
.
Proof. If G is cyclic or
![]() $\exp (G) = p$
, then
$\exp (G) = p$
, then
![]() $n_G = \exp (G)$
by Lemmas 2.3 and 2.2. Moreover, if
$n_G = \exp (G)$
by Lemmas 2.3 and 2.2. Moreover, if
![]() $G \simeq D_{2^{\alpha +1}}$
, then G has only one cyclic subgroup of order
$G \simeq D_{2^{\alpha +1}}$
, then G has only one cyclic subgroup of order
![]() $2^{\alpha }$
while all the other cyclic subgroups have order
$2^{\alpha }$
while all the other cyclic subgroups have order
![]() $2$
, which implies
$2$
, which implies
![]() $n_G = \exp (G)$
.
$n_G = \exp (G)$
.
Now assume that
![]() $n_G = \exp (G)$
. If G is abelian then G is either cyclic or elementary abelian by Proposition 2.5. Now assume that G is neither abelian nor of exponent p. From Theorem 2.6 we have to analyse two cases. First assume that G is isomorphic to
$n_G = \exp (G)$
. If G is abelian then G is either cyclic or elementary abelian by Proposition 2.5. Now assume that G is neither abelian nor of exponent p. From Theorem 2.6 we have to analyse two cases. First assume that G is isomorphic to
![]() $M_{p^{\alpha + 1}}$
. Then
$M_{p^{\alpha + 1}}$
. Then
![]() $(yx)^p = x^{({p(p-1)}/{2})p^{\alpha -1}+p}$
, which yields a contradiction. Indeed, when p is odd, we have
$(yx)^p = x^{({p(p-1)}/{2})p^{\alpha -1}+p}$
, which yields a contradiction. Indeed, when p is odd, we have
![]() $(yx)^p = x^p$
and
$(yx)^p = x^p$
and
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (x^p)|> \exp (G)$
as
$|{\mathcal {I}}_{{\mathcal {C}}} (x^p)|> \exp (G)$
as
![]() $x^p$
is connected to every element of
$x^p$
is connected to every element of
![]() $\langle x \rangle $
and to every element of
$\langle x \rangle $
and to every element of
![]() $\langle yx \rangle $
. If
$\langle yx \rangle $
. If
![]() $p=2$
, then
$p=2$
, then
![]() $(yx)^2 = x^{2^{\alpha - 1} +2}$
and
$(yx)^2 = x^{2^{\alpha - 1} +2}$
and
![]() ${\mathcal {I}}_{{\mathcal {C}}}(x^{2^{\alpha -1} + 2})$
contains more than
${\mathcal {I}}_{{\mathcal {C}}}(x^{2^{\alpha -1} + 2})$
contains more than
![]() $2^{\alpha }$
elements.
$2^{\alpha }$
elements.
Finally, assume that
![]() $p = 2$
and G isomorphic to
$p = 2$
and G isomorphic to
![]() $S_{2^{\alpha + 1}}$
. Then
$S_{2^{\alpha + 1}}$
. Then
![]() $(yx)^2 = x^{2^{\alpha -1}}$
and
$(yx)^2 = x^{2^{\alpha -1}}$
and
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (yx)|> \exp (G)$
.
$|{\mathcal {I}}_{{\mathcal {C}}} (yx)|> \exp (G)$
.
We are now in a position to prove Theorem 1.1.
Proof of Theorem 1.1.
By Lemmas 2.2 and 2.3 and Proposition 2.7, we only need to prove that if
![]() $n_G=\exp (G)$
then G is either cyclic, or
$n_G=\exp (G)$
then G is either cyclic, or
![]() $\exp (G)=p$
, or G is a dihedral
$\exp (G)=p$
, or G is a dihedral
![]() $2$
-group. Thus, let
$2$
-group. Thus, let
![]() $n_G=\exp (G)$
, and by way of contradiction assume neither that G is cyclic, nor
$n_G=\exp (G)$
, and by way of contradiction assume neither that G is cyclic, nor
![]() $\exp (G) = p$
, nor G is a dihedral group of order
$\exp (G) = p$
, nor G is a dihedral group of order
![]() $2^{\exp (G) + 1}$
, such that G has minimal order. Hence, there exists an element
$2^{\exp (G) + 1}$
, such that G has minimal order. Hence, there exists an element
![]() $x \in G$
such that
$x \in G$
such that
![]() $p < o(x) = \exp (G)$
. By Proposition 2.7, it follows that
$p < o(x) = \exp (G)$
. By Proposition 2.7, it follows that
![]() $p \cdot o(x) < |G|$
, and thus G contains a proper subgroup H such that
$p \cdot o(x) < |G|$
, and thus G contains a proper subgroup H such that
![]() $x \in H$
and
$x \in H$
and
![]() $|H|=p\cdot o(x)$
. Then
$|H|=p\cdot o(x)$
. Then
![]() $\exp (H) = \exp (G)$
and H has a cyclic subgroup of index p. By Proposition 2.7, H is a dihedral group of order
$\exp (H) = \exp (G)$
and H has a cyclic subgroup of index p. By Proposition 2.7, H is a dihedral group of order
![]() $2 \exp (G)$
since H is neither cyclic nor such that
$2 \exp (G)$
since H is neither cyclic nor such that
![]() $\exp (H) = p$
. As a consequence G is a
$\exp (H) = p$
. As a consequence G is a
![]() $2$
-group, and by minimality,
$2$
-group, and by minimality,
![]() $|G:H|=2$
. If
$|G:H|=2$
. If
![]() $o(x)=4$
, then
$o(x)=4$
, then
![]() $|G|=16$
and an easy computation using GAP shows that this is a contradiction. Hence, we may assume
$|G|=16$
and an easy computation using GAP shows that this is a contradiction. Hence, we may assume
![]() $o(x)>4$
. Now assume that there exists an element
$o(x)>4$
. Now assume that there exists an element
![]() $a \in G \setminus H$
such that
$a \in G \setminus H$
such that
![]() $o(a)>4$
. Then
$o(a)>4$
. Then
![]() $a^2 \in H$
and
$a^2 \in H$
and
![]() $o(a^2)>2$
. This implies that
$o(a^2)>2$
. This implies that
![]() $a^2 \in \langle x \rangle $
and
$a^2 \in \langle x \rangle $
and
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (a^2)|> \exp (G)$
. Hence, we may assume that
$|{\mathcal {I}}_{{\mathcal {C}}} (a^2)|> \exp (G)$
. Hence, we may assume that
![]() $o(a) \leq 4$
for all
$o(a) \leq 4$
for all
![]() $a \in G \setminus H$
. First assume that
$a \in G \setminus H$
. First assume that
![]() $G \setminus H$
contains an element a of order
$G \setminus H$
contains an element a of order
![]() $2$
. If a does not invert x, then
$2$
. If a does not invert x, then
![]() $(xa)^2=xx^a$
is a nontrivial element of
$(xa)^2=xx^a$
is a nontrivial element of
![]() $\langle x \rangle $
, since
$\langle x \rangle $
, since
![]() $\langle x \rangle $
is normal in G. As a consequence,
$\langle x \rangle $
is normal in G. As a consequence,
![]() $|{\mathcal {I}}_{{\mathcal {C}}} ((xa)^2)|> \exp (G)$
. Now assume that
$|{\mathcal {I}}_{{\mathcal {C}}} ((xa)^2)|> \exp (G)$
. Now assume that
![]() $x^a=x^{-1}$
. Let
$x^a=x^{-1}$
. Let
![]() $b \in H$
be such that
$b \in H$
be such that
![]() $x^b=x^{-1}$
. Then
$x^b=x^{-1}$
. Then
![]() $x^{ab}=x$
and
$x^{ab}=x$
and
![]() $ab$
belongs to the centraliser in G of x. Thus,
$ab$
belongs to the centraliser in G of x. Thus,
![]() $(xab)^4=x^4 \neq 1$
, and
$(xab)^4=x^4 \neq 1$
, and
![]() $|{\mathcal {I}}_{{\mathcal {C}}} (x^4)|> \exp (G)$
. Therefore, we only need to address the case in which
$|{\mathcal {I}}_{{\mathcal {C}}} (x^4)|> \exp (G)$
. Therefore, we only need to address the case in which
![]() $o(a)=4$
for every
$o(a)=4$
for every
![]() $a \in G \setminus H$
. If
$a \in G \setminus H$
. If
![]() $a^2 \in \langle x \rangle $
for some
$a^2 \in \langle x \rangle $
for some
![]() $a \in G \setminus H$
, then
$a \in G \setminus H$
, then
![]() $|{\mathcal {I}}_{{\mathcal {C}}}(a^2)|> \exp (G)$
. This implies that
$|{\mathcal {I}}_{{\mathcal {C}}}(a^2)|> \exp (G)$
. This implies that
![]() $a^2 \in H \setminus \langle x \rangle $
. As a consequence
$a^2 \in H \setminus \langle x \rangle $
. As a consequence
![]() $a^2$
inverts x. On the other hand, the dihedral groups have no automorphisms of order
$a^2$
inverts x. On the other hand, the dihedral groups have no automorphisms of order
![]() $4$
whose square inverts its element of maximal order (see, for instance, Theorem 34.8(a) of [Reference Berkovich4]). This final contradiction proves the theorem.
$4$
whose square inverts its element of maximal order (see, for instance, Theorem 34.8(a) of [Reference Berkovich4]). This final contradiction proves the theorem.
Acknowledgement
This work was carried out during the second author’s visit to Kent State University. He wishes to thank the Department of Mathematical Science for its excellent hospitality.


