Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-31T07:22:47.287Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLE SOLUTIONS FOR A KIRCHHOFF EQUATION WITH NONLINEARITY HAVING ARBITRARY GROWTH

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  13 March 2017

MARCELO F. FURTADO Open the ORCID record for MARCELO F. FURTADO [Opens in a new window]  and
HENRIQUE R. ZANATA
MARCELO F. FURTADO*
Affiliation:
Departamento de Matemática, Universidade de Brasília, 70910-900, Brasília-DF, Brazil email mfurtado@unb.br
HENRIQUE R. ZANATA
Affiliation:
Departamento de Matemática, Universidade de Brasília, 70910-900, Brasília-DF, Brazil email h.r.zanata@mat.unb.br
*
✉ mfurtado@unb.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the existence of infinitely many solutions 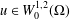$u\in W_{0}^{1,2}(\unicode[STIX]{x1D6FA})$ for the Kirchhoff equation

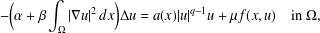$$\begin{eqnarray}\displaystyle -\biggl(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D6FB}u|^{2}\,dx\biggr)\unicode[STIX]{x1D6E5}u=a(x)|u|^{q-1}u+\unicode[STIX]{x1D707}f(x,u)\quad \text{in }\unicode[STIX]{x1D6FA}, & & \displaystyle \nonumber\end{eqnarray}$$
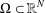where $\unicode[STIX]{x1D6FA}\subset \mathbb{R}^{N}$ is a bounded smooth domain, 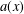$a(x)$ is a (possibly) sign-changing potential, 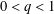$0<q<1$ , 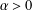$\unicode[STIX]{x1D6FC}>0$ , 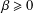$\unicode[STIX]{x1D6FD}\geq 0$ , 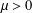$\unicode[STIX]{x1D707}>0$ and the function 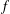$f$ has arbitrary growth at infinity. In the proof, we apply variational methods together with a truncation argument.

Keywords

Kirchhoff equationinfinitely many solutionsvariational methodtruncation argument

MSC classification

Primary: 35J20: Variational methods for second-order elliptic equations
Secondary: 35J25: Boundary value problems for second-order elliptic equations 35J60: Nonlinear elliptic equations

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 98 - 109
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was partially supported by the National Council for Scientific and Technological Development (CNPq), Brazil.

References

Agmon, S., Douglis, A. and Nirenberg, L., ‘Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary value conditions. I’, Comm. Pure Appl. Math. 12 (1959), 623–727.CrossRefGoogle Scholar
Alves, C. O., Corrêa, F. J. S. A. and Ma, T. F., ‘Positive solutions for a quasilinear elliptic equation of Kirchhoff type’, Comput. Math. Appl. 49 (2005), 85–93.CrossRefGoogle Scholar
Ambrosetti, A., Brezis, H. and Cerami, G., ‘Combined effects of concave and convex nonlinearities in some elliptic problems’, J. Funct. Anal. 122 (1994), 519–543.CrossRefGoogle Scholar
Chu, C.-M., ‘Multiplicity of positive solutions for Kirchhoff type problem involving critical exponent and sign-changing weight functions’, Bound. Value Probl. 2014 (2014), Article ID 19.CrossRefGoogle Scholar
Clark, D. C., ‘A variant of the Ljusternik–Schnirelmann theory’, Indiana Univ. Math. J. 22 (1972), 65–74.CrossRefGoogle Scholar
Figueiredo, G. M. and Santos Junior, J. R., ‘Multiplicity of solutions for a Kirchhoff equation with subcritical or critical growth’, Differential Integral Equations 25(9–10) (2012), 853–868.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N., Elliptic Partial Differential Equations of Second Order (Springer, Berlin, 1983).Google Scholar
Guo, Z., ‘Elliptic equations with indefinite concave nonlinearities near the origin’, J. Math. Anal. Appl. 367 (2010), 273–277.CrossRefGoogle Scholar
Heinz, H. P., ‘Free Ljusternik–Schnirelmann theory and the bifurcation diagrams of certain singular nonlinear systems’, J. Differential Equations 66 (1987), 263–300.CrossRefGoogle Scholar
Kirchhoff, G., Mechanik (Teubner, Leipzig, 1883).Google Scholar
Lions, J.-L., ‘On some questions in boundary value problems of mathematical physics’, in: Contemporary Developments in Continuum Mechanics and Partial Differential Equations (Proc. Int. Sympos., Inst. Mat., Univ. Fed. Rio de Janeiro, Rio de Janeiro, 1977), North-Holland Mathematical Studies, 30 (North-Holland, Amsterdam, 1978), 284–346.Google Scholar
Wang, Z.-Q., ‘Nonlinear boundary value problems with concave nonlinearities near the origin’, NoDEA Nonlinear Differential Equations Appl. 8 (2001), 15–33.CrossRefGoogle Scholar
Yijing, S. and Xing, L., ‘Existence of positive solutions for Kirchhoff type problems with critical exponent’, J. Partial Differ. Equ. 25(2) (2012), 85–96.Google Scholar