Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-31T22:52:47.206Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CATEGORIFICATION OF THE KAUFFMAN BRACKET SKEIN MODULE OF 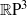$ \mathbb{R} {\mathrm{P} }^{3} $

Part of: Low-dimensional topology Differential topology

Published online by Cambridge University Press:  11 April 2013

BOŠTJAN GABROVŠEK
BOŠTJAN GABROVŠEK*
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Jadranska ulica 19, SI-1000 Ljubljana, Slovenia email bostjan.gabrovsek@fmf.uni-lj.si
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Khovanov homology, an invariant of links in 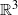${ \mathbb{R} }^{3} $, is a graded homology theory that categorifies the Jones polynomial in the sense that the graded Euler characteristic of the homology is the Jones polynomial. Asaeda et al. [‘Categorification of the Kauffman bracket skein module of 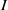$I$-bundles over surfaces’, Algebr. Geom. Topol. 4 (2004), 1177–1210]generalised this construction by defining a double graded homology theory that categorifies the Kauffman bracket skein module of links in 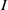$I$-bundles over surfaces, except for the surface 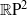$ \mathbb{R} {\mathrm{P} }^{2} $, where the construction fails due to strange behaviour of links when projected to the nonorientable surface 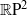$ \mathbb{R} {\mathrm{P} }^{2} $. This paper categorifies the missing case of the twisted 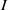$I$-bundle over 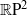$ \mathbb{R} {\mathrm{P} }^{2} $, 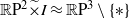$ \mathbb{R} {\mathrm{P} }^{2} \widetilde {\times } I\approx \mathbb{R} {\mathrm{P} }^{3} \setminus \{ \ast \} $, by redefining the differential in the Khovanov chain complex in a suitable manner.

Keywords

Khovanov homologycategorificationskein moduleKauffman bracket

MSC classification

Secondary: 57M27: Invariants of knots and 3-manifolds 57M25: Knots and links in $S^3$ 57R56: Topological quantum field theories

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 407 - 422
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Asaeda, M. M., Przytycki, J. H. and Sikora, A. S., ‘Categorification of the Kauffman bracket skein module of $I$-bundles over surfaces’, Algebr. Geom. Topol. 4 (2004), 1177–1210.CrossRefGoogle Scholar
Bar-Natan, D., ‘On Khovanov’s categorification of the Jones polynomial’, Algebr. Geom. Topol. 2 (2002), 337–370.CrossRefGoogle Scholar
Drobotukhina, Yu. V., ‘An analogue of the Jones polynomial for links in $ \mathbb{R} {P}^{3} $ and a generalization of the Kauffman-Murasugi theorem’, Algebra i Analiz 2 (3) (1990), 171–191.Google Scholar
Hoste, J. and Przytycki, J. H., ‘The $(2, \infty )$-skein module of lens spaces; a generalization of the Jones polynomial’, J. Knot Theory Ramifications 2 (3) (1993), 321–333.CrossRefGoogle Scholar
Hoste, J. and Przytycki, J. H., ‘The Kauffman bracket skein module of ${S}^{1} \times {S}^{2} $’, Math. Z. 220 (1) (1995), 63–73.Google Scholar
Khovanov, M., ‘A categorification of the Jones polynomial’, Duke Math. J. 101 (3) (2000), 359–426.CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., ‘Khovanov homology is an unknot-detector’. arXiv:1005.4346v1 [math.GT], 2010.Google Scholar
Manturov, V. O., ‘Khovanov homology for virtual knots with arbitrary coefficients’, Izv. Math. 71 (5) (2007), 967–999.CrossRefGoogle Scholar
Mroczkowski, M., ‘Kauffman bracket skein module of the connected sum of two projective spaces’, J. Knot Theory Ramifications 20 (5) (2011), 651–675.Google Scholar
Mroczkowski, M. and Dabkowski, M. K., ‘KBSM of the product of a disk with two holes and ${S}^{1} $’, Topology Appl. 156 (10) (2009), 1831–1849.CrossRefGoogle Scholar
Przytycki, J. H., ‘Fundamentals of Kauffman bracket skein modules’, Kobe J. Math. 16 (1) (1999), 45–66.Google Scholar
Przytycki, J. H., ‘Skein modules of 3-manifolds’, Bull. Pol. Acad. Sci. 39 (1–2) (1991), 91–100.Google Scholar
Turaev, V. G., ‘The Conway and Kauffman modules of the solid torus’, J. Soviet Math. 52 (1990), 2799–2805.Google Scholar