Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-30T19:18:55.062Z Has data issue: false hasContentIssue false
  • English
  • Français

ARITHMETIC PROPERTIES OF AN ANALOGUE OF t-CORE PARTITIONS

Part of: Additive number theory; partitions Discontinuous groups and automorphic forms Combinatorics

Published online by Cambridge University Press:  03 June 2024

PRANJAL TALUKDAR Open the ORCID record for PRANJAL TALUKDAR [Opens in a new window]
PRANJAL TALUKDAR*
Affiliation:
Department of Mathematical Sciences, Tezpur University, Napaam 784028, Assam, India
*
e-mail: pranjaltalukdar113@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

An integer partition of a positive integer n is called t-core if none of its hook lengths is divisible by t. Gireesh et al. [‘A new analogue of t-core partitions’, Acta Arith. 199 (2021), 33–53] introduced an analogue 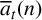$\overline {a}_t(n)$ of the t-core partition function. They obtained multiplicative formulae and arithmetic identities for 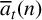$\overline {a}_t(n)$ where 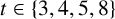$t \in \{3,4,5,8\}$ and studied the arithmetic density of 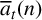$\overline {a}_t(n)$ modulo 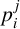$p_i^{\,j}$ where 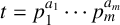$t=p_1^{a_1}\cdots p_m^{a_m}$ and 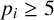$p_i\geq 5$ are primes. Bandyopadhyay and Baruah [‘Arithmetic identities for some analogs of the 5-core partition function’, J. Integer Seq. 27 (2024), Article no. 24.4.5] proved new arithmetic identities satisfied by 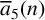$\overline {a}_5(n)$. We study the arithmetic densities of 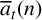$\overline {a}_t(n)$ modulo arbitrary powers of 2 and 3 for 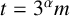$t=3^\alpha m$ where 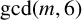$\gcd (m,6)$=1. Also, employing a result of Ono and Taguchi [‘2-adic properties of certain modular forms and their applications to arithmetic functions’, Int. J. Number Theory 1 (2005), 75–101] on the nilpotency of Hecke operators, we prove an infinite family of congruences for 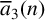$\overline {a}_3(n)$ modulo arbitrary powers of 2.

Keywords

t-core partitionanalogue of t-core partitiontheta functionmodular formarithmetic density

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers 11F11: Holomorphic modular forms of integral weight

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 1 , February 2025 , pp. 68 - 79
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author was partially supported by the Council of Scientific and Industrial Research (CSIR), Government of India, under the CSIR-JRF scheme (Grant No. 09/0796(12991)/2021-EMR-I).

References

Anderson, J., ‘An asymptotic formula for the $t$ -core partition function and a conjecture of Stanton’, J. Number Theory 128 (2008), 2591–2615.CrossRefGoogle Scholar
Bandyopadhyay, S. and Baruah, N. D., ‘Arithmetic identities for some analogs of the 5-core partition function’, J. Integer Seq. 27 (2024), Article no. 24.4.5.Google Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer-Verlag, New York, 1991).CrossRefGoogle Scholar
Cho, H., Kim, B., Nam, H. and Sohn, J., ‘A survey on $t$ -core partitions’, Hardy–Ramanujan J. 44 (2022), 81–101.Google Scholar
Cotron, T., Michaelsen, A., Stamm, E. and Zhu, W., ‘Lacunary eta-quotients modulo powers of primes’, Ramanujan J. 53 (2020), 269–284.CrossRefGoogle Scholar
Garvan, F., Kim, D. and Stanton, D., ‘Cranks and $t$ -cores’, Invent. Math. 101 (1990), 1–17.CrossRefGoogle Scholar
Gireesh, D. S., Ray, C. and Shivashankar, C., ‘A new analogue of $t$ -core partitions’, Acta Arith. 199 (2021), 33–53.Google Scholar
Granville, A. and Ono, K., ‘Defect zero $p$ -blocks for finite simple groups’, Trans. Amer. Math. Soc. 348 (1996), 331–347.CrossRefGoogle Scholar
Hardy, G. H. and Ramanujan, S., ‘Asymptotic formulae in combinatory analysis’, Proc. Lond. Math. Soc. (3) 17 (1918), 75–115.CrossRefGoogle Scholar
Jindal, A. and Meher, N. K., ‘Arithmetic density and congruences of $t$ -core partitions’, Results Math. 79 (2024), Article no. 4, 23 pages.CrossRefGoogle Scholar
Koblitz, N., Introduction to Elliptic Curves and Modular Forms (Springer-Verlag, New York, 1991).Google Scholar
Ono, K., The Web of Modularity: Arithmetic of the Coefficients of Modular Forms and $q$ -series, CBMS Regional Conference Series in Mathematics, 102 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Ono, K. and Taguchi, Y., ‘2-adic properties of certain modular forms and their applications to arithmetic functions’, Int. J. Number Theory 1 (2005), 75–101.CrossRefGoogle Scholar
Radu, S. and Sellers, J. A., ‘Congruence properties modulo 5 and 7 for the pod function’, Int. J. Number Theory 7 (2011), 2249–2259.CrossRefGoogle Scholar
Serre, J.-P., ‘Divisibilité de certaines fonctions arithmétiques’, Sém. Delange-Pisot-Poitou, Théor. Nombres 16 (1974), 1–28.Google Scholar
Serre, J.-P., ‘Valeurs propres des opérateurs de Hecke modulo $\ell$ ’, Astérisque 24 (1975), 109–117.Google Scholar
Tate, J., ‘The non-existence of certain Galois extensions of $\mathbb{Q}$ unramified outside 2’, in: Arithmetic Geometry, Contemporary Mathematics, 174 (eds. Childress, N. and Jones, J. W.) (American Mathematical Society, Providence, RI, 1994), 153–156.CrossRefGoogle Scholar