Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-29T11:15:57.718Z Has data issue: false hasContentIssue false
  • English
  • Français

A GENERALISATION OF A THEOREM OF ERDŐS AND NIVEN

Part of: Multiplicative number theory Sequences and sets

Published online by Cambridge University Press:  24 January 2022

XIAO JIANG  and
SHAOFANG HONG
XIAO JIANG
Affiliation:
Mathematical College, Sichuan University, Chengdu 610064, P. R. China e-mail: 2019322010001@stu.scu.edu.cn
SHAOFANG HONG*
Affiliation:
Mathematical College, Sichuan University, Chengdu 610064, P. R. China e-mail: s-f.hong@tom.com
*
e-mail: sfhong@scu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1946, Erdős and Niven proved that no two partial sums of the harmonic series can be equal. We present a generalisation of the Erdős–Niven theorem by showing that no two partial sums of the series 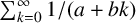$\sum _{k=0}^\infty {1}/{(a+bk)}$ can be equal, where a and b are positive integers. The proof of our result uses analytic and p-adic methods.

Keywords

p-adic valuationarithmetic progressionpartial sumharmonic seriesDiophantine equationunit fraction

MSC classification

Primary: 11B25: Arithmetic progressions
Secondary: 11B75: Other combinatorial number theory 11B83: Special sequences and polynomials 11N13: Primes in progressions

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 215 - 223
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

S. F. Hong was supported partially by National Science Foundation of China, Grant #12171332.

References

Chen, Y. G. and Tang, M., ‘On the elementary symmetric functions of $1,1/ 2,\dots, 1/ n$ ’, Amer. Math. Monthly 119 (2012), 862–867.CrossRefGoogle Scholar
Erdős, P. and Niven, I., ‘Some properties of partial sums of the harmonic series’, Bull. Amer. Math. Soc. (N.S.) 52 (1946), 248–251.CrossRefGoogle Scholar
Feng, Y. L., Hong, S. F., Jiang, X. and Yin, Q. Y., ‘A generalization of a theorem of Nagell’, Acta Math. Hungar. 157 (2019), 522–536.CrossRefGoogle Scholar
Hong, S. F. and Wang, C. L., ‘The elementary symmetric functions of reciprocals of the elements of arithmetic progressions’, Acta Math. Hungar. 144 (2014), 196–211.CrossRefGoogle Scholar
Koblitz, N., $p$ -adic Numbers, $p$ -adic Analysis and Zeta-Functions, Graduate Texts in Mathematics, 58 (Springer, New York, 1984).Google Scholar
Luo, Y. Y., Hong, S. F., Qian, G. Y. and Wang, C. L., ‘The elementary symmetric functions of a reciprocal polynomial sequence’, C. R. Math. Acad. Sci. Paris, Ser. I 352 (2014), 269–272.CrossRefGoogle Scholar
Nagell, T., ‘Eine Eigenschaft gewissen Summen’, Skr. Norske Vid. Akad. Kristiania 13 (1923), 10–15.Google Scholar
Shorey, T. N. and Tijdeman, R., ‘On the greatest prime factor of an arithmetical progression’, in: A Tribute to Paul Erdős (eds. Baker, A., Bollabás, B. and Hajnal, A.) (Cambridge University Press, Cambridge, 1990), 385–389.CrossRefGoogle Scholar
Theisinger, L., ‘Bemerkung über die harmonische Reihe’, Monatsh. Math. Phys. 26 (1915), 132–134.CrossRefGoogle Scholar
Wang, C. L. and Hong, S. F., ‘On the integrality of the elementary symmetric functions of $1,1/ 3,\dots, 1/ \left(2n-1\right)$ ’, Math. Slovaca 65 (2015), 957–962.CrossRefGoogle Scholar