The horizon ξ T (x) of a random field ζ (x, y) of right circular cones on a plane is investigated. It is supposed that bases of cones are centered at points sn = (xn , yn ), n = 1, 2, ···, on the (X, Y)-plane, constituting a Poisson point process S with intensity λ0 > 0 in a strip ΠT = {(x, y): – ∞< x <∞, 0 ≦ y ≦ T}, while altitudes of the cones h 1, h 2, · ·· are of the form hn = hn * + f(yn ), n = 1, 2, ···, where f(y) is an increasing continuous function on [0,∞), f(0) = 0, and h 1*, h 2*, · ·· is a sequence of i.i.d. positive random variables which are independent of the Poisson process S and have a distribution function F(h) with density p(h).

Let 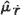denote the expected mean number of local maxima of the process ξ T (x) per unit length of the X-axis. We obtain an exact formula for 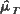under an arbitrary trend function f(y). Conditions sufficient for the limit 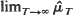being infinite are obtained in two cases: (a) h 1* has the uniform distribution in [0, H], f(y) = ky γ; (b) h 1* has the Rayleigh distribution, f(y) = k[log(y + 1)]γ . (In both cases γ 0 and 0 < k∞.) The corresponding sufficient conditions are: 0 < γ< 1 in case (a), 0 < γ< 1/2 in case (b).